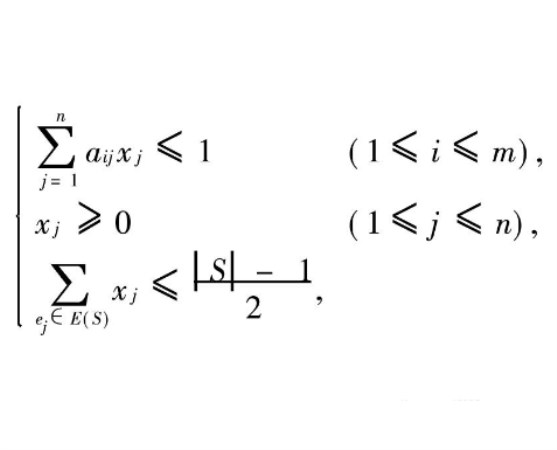匹配多面體

匹配多面體(matching polytope)是一類組合構形，它是由一個圖的所有對集相應的向量所形成的凸包。

基本介紹

• 中文名：匹配多面體
• 外文名：matching polytope
• 所屬學科：數學
• 所屬問題：組合學（組合多面形)
• 簡介：一類組合構形

基本介紹

設圖，V和E分別為G的節點集和邊集，且記和，對於E的任何一個子集E′，它的相應向量，其中，當；否則，，若為G的節點與邊之間的關聯陣，即，當v_i為e_j的一個端點；否則，，則匹配多面體由下面的不等式組的解集所確定：

其中，S為V的子集且含有奇數個節點，E(S)為由S在G上的導出子圖的邊集。

相關介紹

對圖 ，一個邊子集 ，若使圖中每個點只關聯於X中的一條邊，則稱X是G的一個匹配。一個邊子集 ，若使圖中每個點只關聯於X中的兩條邊，則稱X是G的一個2-匹配(2-Matching)，我們用x表示邊子集也表示它的關聯向量，用 表示x的分量，其中e是一條邊，讓A表示G的點邊關聯矩陣，則

匹配問題可表示為如下形式：

{ ，x是整數向量}。

2-匹配問題可表示為如下形式：

{ ，x是0，1向量)．

一個點子集 ，若它所含的點數 是奇數，則稱T為奇點集，定義

性質1 圖G的匹配的凸包為：

奇點集

這就是著名的Edmonds-匹配多面體(Edmonds matching polyhedron)。

設x是任意2-匹配的關聯向量，則對任意的子集 ，以及 ，有關係

因此

另一方面，因為

因此，數值 是偶數。現在若|F|是奇數，則有

即

因而有

圖1

通常稱二元組“S，F”(，|F|是奇數)為一個“梳子”(comb)，稱關係式(4)為一個梳子不等式。最簡單的梳子不等式為如下形式

稱其為“三角形梳子”(triangular comb)(因S中點形成的子圖為三角形)。

性質2 圖G的2-匹配的凸包為