基本介紹
- 中文名:s匹配
- 外文名:s-matching
- 所屬學科:數學
- 所屬問題:組合學(圖與超圖)
- 簡介:匹配的推廣
基本介紹,相關介紹,
基本介紹
設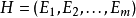 為
為 上的一個超圖,它的關聯矩陣為
上的一個超圖,它的關聯矩陣為 ,n和m分別為H的階和度,給定一個向量
,n和m分別為H的階和度,給定一個向量 ,即
,即 均為非負整數,H的一個s匹配就是指多面體Q(s)上的一個所有分量均為整數的向量
均為非負整數,H的一個s匹配就是指多面體Q(s)上的一個所有分量均為整數的向量 ,其中,
,其中, ,而y表示向量y的轉置,當
,而y表示向量y的轉置,當 時,即
時,即 ,y的分量只能取0或1,也就是說,任何一個節點至多包含在一條相應y的分量為1的邊中,所有相應1n匹配y的分量為1的邊的集合就是H的一個匹配,對應超圖的每一條邊Ej給定一個整數
,y的分量只能取0或1,也就是說,任何一個節點至多包含在一條相應y的分量為1的邊中,所有相應1n匹配y的分量為1的邊的集合就是H的一個匹配,對應超圖的每一條邊Ej給定一個整數 ,稱dj為邊Ej的權,記
,稱dj為邊Ej的權,記 ,H上s匹配的最大權定義為
,H上s匹配的最大權定義為
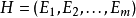











相關介紹





1.多面體 上的所有極點都是整向量,即所有分量皆為整數;
上的所有極點都是整向量,即所有分量皆為整數;

2.對任何 皆為整數;
皆為整數;

3.對任何 ,均有
,均有








