加權函式法

加權函式法是通過給離散化的激勵函式Foutier譜係數賦予一個加權函式，從而將產生長期項的某個鄰域內的頻率項係數消去，以達到消除長期項的目的。

基本介紹

• 中文名：加權函式法
• 外文名：Weighting function method

介紹

一般定義

在離散設定中，權重函式 是在離散集 上定義的正函式，其通常是有限的或可數的。 權重函式 對應於所有元素具有相等權重的未加權情況。 然後可以將這個權重套用於各種概念。

如果函式 是實值函式，則 的未加權和 定義為：

但是給定權重函式 ，加權和或錐形組合定義為:

加權和的一個常見套用出現數值積分中。如果 是 的有限子集，則可以替換未加權的基數 的加權基數:

如果 是有限的非空集，則可以替換未加權的均值或平均值:

按加權平均值或加權平均值計算:

在這種情況下，只有相對權重是相關的。

統計學

加權平均值通常用於統計中以補償偏差的存在。對於具有方差 的多個獨立時間 測量的量 ，通過對權重 的所有測量求平均來獲得信號的最佳估計，並且得到的方差小於每個獨立測量值 無線網路。最大似然法使用相同的權重 對擬合和數據之間的差異進行加權。

隨機變數的期望值是它可能採用的可能值的加權平均值，權重是相應的機率。更一般地，隨機變數的函式的期望值是函式對於隨機變數的每個可能值所採用的值的機率加權平均值。

在假設因變數受獨立變數的當前和滯後（過去）值影響的回歸中，估計分布滯後函式，該函式是當前和各種滯後自變數值的加權平均值。類似地，移動平均模型將演化變數指定為當前的加權平均值和隨機變數的各種滯後值。

機械學

術語加權函式來自力學：如果一個槓桿上有n個對象的集合，權重為 ，...， （其中權重在物理意義上被解釋）和位置： ，...， ，那么 如果槓桿的支點位於質量中心，槓桿將處於平衡狀態:

這也是位置 的加權平均值。

加權函式法的魯棒跟蹤設計

不確定系統的信號跟蹤、系統的穩定性和干擾抑制問題，三者與控制性能指標設計問題之間是可相互轉化的。跟蹤控制問題的示意圖，如圖1所示。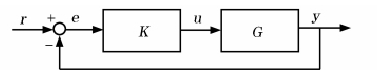

圖1

圖1中， 為系統參考信號輸入； 為誤差; 為系統輸出。

定義 1 從到的閉環傳遞函式為靈敏度函式 ; 從 到 的閉環傳遞函式為 為補靈敏度函式。

靈敏度函式 與系統抗干擾能力有關; 補靈敏度函式 與系 統魯棒穩定性有關，由於 + ，所以提高系統的抗干擾能力與提高系統的魯棒穩定性的要求兩者相矛盾，對兩者進行折衷，就是混合靈敏度最佳化問題。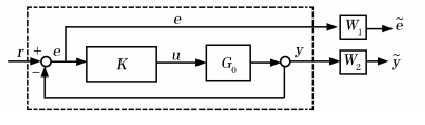

圖2

為了解決上述矛盾，通常選擇加權函式 和 對 和 進行頻域整形，在低頻段以減少靈敏度函式的增益為主，而在高頻段以減少補靈敏度函式的增益為主。當被控對象 存在不確定攝動 ，為了有效抑制干擾，將圖1的跟蹤問題，信號跟蹤加權函式，如圖 2 所示。

圖2中, 為標稱被控對象; 和 分別為系統輸入信號誤差和系統輸出的整形過濾器函式，分別設定為低通濾波器和高通濾波器。