力向量是一個物理學術語。
基本介紹
- 中文名:力向量/力矢量
- 外文名:Force vector / force vector

力向量是一個物理學術語。

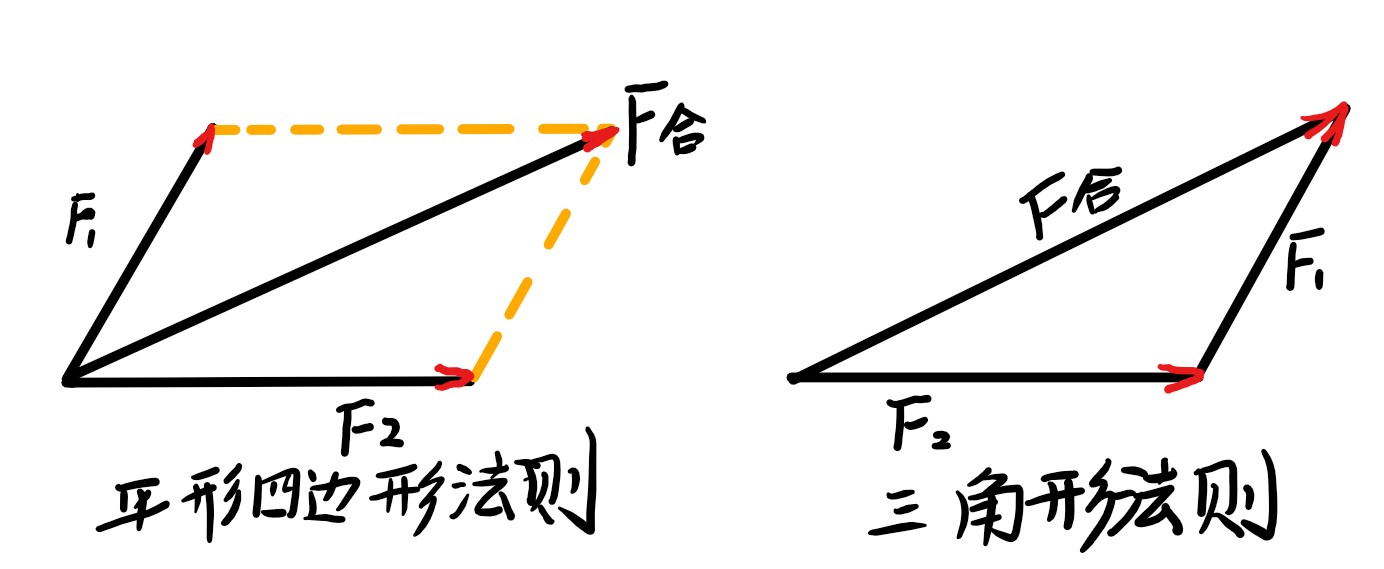
力向量是一個物理學術語。在生活中,我們都有這樣的認識,當一個物體受到多個力的作用時,這個物體受的合力效果,不但與這些力的大小有關,還與這些力的方向有關。例如兩人推車,一個將車向右推,一個向左推,這時兩人推車的速度,比一個...
換算成正東正南正西正北四個方向的力的向量,如果四個向量不等大,就會產生離心運動,或者會俗稱的震動離心擺動。飛機旋翼的設計會涉及到,或是飛機轉子都會涉及到。離心力公式 (旋轉體離心運動的r·v,r0為旋轉體旋轉半徑r0)r/v^2=r0/v0^2=m0/F0=1/a,v^2=(F向*r0)/m,r=r0 ...
向量,最初被套用於物理學。很多物理量如力、速度、位移以及電場強度、磁感應強度等都是向量。大約公元前350年前,古希臘著名學者亞里士多德就知道了力可以表示成向量,兩個力的組合作用可用著名的平行四邊形法則來得到。“向量”一詞來自力學、解析幾何中的有向線段。最先使用有向線段表示向量的是英國大科學家牛頓...
發動機推力向量控制 發動機推力向量控制是軍事名詞。發動機推力向量控制,改變飛行器發動機推力方向以產生控制力矩,使飛行器作俯仰偏航或滾動運動,以保證飛行器按預定軌道飛行的控制方式。通常由飛行器控制系統發出控制指令,以伺服活門和作動器為執行元件。
推力向量控制還有偏流環、轉動斜置噴管等方式。系統如何控制 根據飛行器控制系統的指令,偏轉發動機噴焰排出方向,使其與飛行器軸線偏斜一定角度召,從而改變反作用推力F的方向,此時,發動機推力F的徑向分量Fsin口就是側向控制力Fs,它圍繞飛行器重心產生一個控制力矩,用於飛行器姿態的穩定與控制。對它的套用,還得依靠...
固定向量 固定向量也叫做膠著向量。在數學上指的是確定方向與大小,以及起點位置的向量。力學中的作用力就是固定向量。定義 固定向量指的是作用於一點的向量(亦稱膠著向量)。數學上不研究固定向量,只研究自由向量。
一個向量只要不改變它的大小和方向,它的起點和終點可以任意平行移動的向量,叫做自由向量。自由向量可以平移至空間任意點,這樣一來,若已知向量的大小和方向,則向量就算給出。例如物體運動時的速度和加速度就是自由向量,在數學中把自由向量,簡稱為向量。 [1] ...
例如勢場f的向量線是它的勢函式的梯度線,即這個勢函式變化最快的線。若f是穩定流動(即與時間無關)的流體的速度場,則它的向量線是流體質點的移動軌跡,稱為流線,若f是引力場,則相應的向量線稱為力線。基本介紹 我們知道,在穩定流動的流體中,質點的瞬時運動方向是該點的速度方向,這就是說,流體中質點的...
物理學中的速度與力的平行四邊形概念是向量理論的一個重要起源之一。18世紀中葉之後,歐拉、拉格朗日、拉普拉斯和柯西等的工作,直接導致了在19世紀中葉向量力學的建立。同時,向量概念是近代數學中重要和基本的概念之一,有著深刻的幾何背景。它始於萊布尼茲的位置幾何。現代向量理論是在複數的幾何表示這條線索上發展起來...
在物理學和工程學中,幾何向量更常被稱為矢量。許多物理量都是矢量,比如一個物體的位移,球撞向牆而對其施加的力等等。與之相對的是標量,即只有大小而沒有方向的量。一些與向量有關的定義亦與物理概念有密切的聯繫,例如向量勢對應於物理中的勢能。幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。
《合成射流技術套用於推力向量控制的機理研究》是依託中國人民解放軍國防科技大學,由夏智勛擔任項目負責人的面上項目。中文摘要 本項目對合成射流技術在推力向量控制中的套用進行探索性研究,通過實驗和數值模擬研究相結合建立合成射流推力向量控制系統的機理、方法以及相應的推力計算方法,建立實驗室規模的合成射流技術演示...
在物理學和工程學中,幾何向量更常被稱為矢量。許多物理量都是矢量,比如一個物體的位移,球撞向牆而對其施加的力等等。與之相對的是標量,即只有大小而沒有方向的量。一些與向量有關的定義亦與物理概念有密切的聯繫,例如向量勢對應於物理中的勢能。幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。
徑向量(radius vector)亦稱向徑,又稱徑矢,一種特殊向量。以原點O為起點,以點M(x,y,z)為終點的向量稱做徑向量,記作r(M),或簡記作 r。由於徑向量的坐標與其終點M的坐標相同,所以它按基本向量的分解為:r=xi+yj+zk。定義 徑向量(radius vector)亦稱向徑,又稱徑矢。一種特殊向量,指始點在坐標...
力矩(moment of force)是力學的基本概念之一,是力使物體繞一點或一軸轉動的狀態發生改變的作用的度量,稱該點為矩心,該軸為矩軸。力對點的矩可表示為向量,它等於由矩心到力作用點所確定的向量和力向量的向量積,如圖1,力F作用點為A,矩心點為O,力對O的力矩為 其大小為 ,式中 是 到 的距離...
建立平面直角坐標系,將物體受到的各個力移動到平面坐標系的原點(共點力),這時可將各個力向量沿x軸和y軸方向進行正交分解,然後再分別沿這兩個方向求出合力,正交分解法是處理多個力作用問題的基本方法,值得注意的是,對方向選擇時,儘可能使較多的力落在方向軸上;被分解的力儘可能是已知力。
舉例 以一個位於斜面上的長方體來說明示力圖。將所有外部的支撐及結構變成外力,此例中的外力包括:(1):是長方體質量及重力加速度的乘積,也就是其重量;(2):斜面上的正向力;(3):斜面上的摩擦力。外力向量均有標示方向及作用點,旁邊也會標示其大小。其中也包括坐標系統,以便於描述外力。
vector potential 矢勢;向量勢 state vector 狀態向量 displacement vector 位移矢量;位移向量 input vector 輸入矢量;輸入向量 gradient vector 梯度向量 wave vector 波矢;波矢量 vector function 向量函式;矢量函式 unit vector 單位向量;單位矢量 force vector 力向量;力矢量 vector quantity 矢量;向量 position ...
矢量又稱“向量”。既有大小、又有方向的量。例如,力、速度、電場強度等物理量都是矢量。只有大小、沒有方向的量稱為標量。例如,距離、面積、溫度等。套用——矢量圖 矢量圖 計算機中顯示的數字圖像可以分為兩大類——矢量圖和點陣圖。矢量圖使用直線和曲線來描述圖形,這些圖形的元素是一些點、線、矩形、多邊形...
線上性代數中,基(也稱為基底)是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集,基的元素稱為基向量。向量空間中任意一個元素,都可以唯一地表示成基向量的線性組合。如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間的維數。定義 設集合S為環R上模A的生成元...
