剪下鎖死

剪下鎖死，又稱剪下閉鎖、剪力自鎖等，是有限元分析過程中經常出現的一種數值問題，一般發生在出現彎曲變形的線性完全積分單元中。此種現象僅影響受彎曲載荷作用的完全積分線性單元，若模型受到的是剪力載荷，則完全積分線性單元的計算結果非常好。

基本介紹

• 中文名：剪下鎖死
• 外文名：shear locking
• 別名：剪下閉鎖、剪力自鎖等
• 領域：數學
• 學科：數學
• 定義：有限元分析中的一種數值問題

概念

剪下鎖死現象一般發生在出現彎曲變形的線性完全積分單元中（例如：CPS4、CPE4、C3D8）。線性單元的直邊不能承受彎曲載荷作用，分析過程中可能出現原本不存在的虛假剪應變，使單元的彎曲剛度過大，計算的位移值偏小，即單元的位移場不能模擬由於彎曲而引起的剪下變形和彎曲變形，這就是所謂的“剪下鎖死”現象。當單元長度與厚度的數量級相同或長度大於厚度時，此現象會更加嚴重。

有限元驗證

一個長1m，截面尺寸為0.1m*0.1m，兩端簡支的梁，中間受一個集中荷載(F=1000N)，結構示意圖如圖所示，材料參數：E=1GPa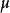， =0.2。依據材料力學，理論解應為。

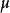
採用四結點四邊形等參單元離散，劃分不同格線密度：在長度方向上等分10份，在厚度方向上分別等分1份、2份、4份和8份，其中對厚度等分8份的情況還進行了水平向等分20份和50份的分析，有限元格線圖如圖所示，取梁中間最下方結點的的豎直向位移與理論解進行對比。

對上述不同有限元格線模型進行分析，採用PLANE182單元默認的積分方式，得到梁中間最下方結點的豎直向位移如表所示，表中ndivX為水平向劃分單元份數，ndivY為梁厚度方向劃分的單元份數。從表中可以看出，只有當梁採用非常密的格線時才能得到與理論解比較接近的值。這說明：1、對這種細長結構，採用實體單元進行離散是非常不經濟的，而採用線性形狀的梁單元只需要很少的單元就能夠得到精確的結果；2、當單元比較少時，由於出現的剪下鎖死現象導致計算結果偏小，這是由於剪力鎖閉消耗了一定的剪下能量，彎曲變形就小了。

格線劃分示意圖

通過上面的分析，我們可以看出在用有限元進行分析時，剪下鎖死現象的確是存在的。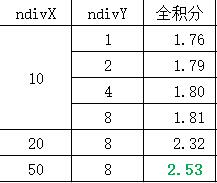

不同方向單元數表

產生原因

離散後的單元長邊與短邊之較大，單元狹長，此時單元承受垂直於長邊的荷載，使單元的變形以彎曲變形為主，板、殼厚度極小而剪下應變接近於零，剪下應變能會被過分誇大，從而導致剪下鎖死。

消除辦法

如果懷疑模型中出現了剪下鎖死現象，可以考慮採用減縮積分單元、非協調單元或高次單元來儘可能的消除這種現象。其中減縮積分單元在一定程度消除剪下鎖死的同時，可能會出現沙漏現象；非協調單元在單元形狀比較畸形時計算結果會非常差；高次單元由於單元節點增加，計算工作量會有很大的提高。

剪下鎖死是否會產生，與結構受力、單元形狀、單元模式選取等多因素相關，若想消除這種現象，需要了解每一種方法的適用範圍、優缺點等，選取合適、正確的方法去進行分析，只有這樣，才能得到合理的計算結果。值得注意的是，僅僅改變單元類型往往不會使計算結果得到很大的改進，劃分格線時應儘可能的保證單元形狀是規則的。