簡介
前序遍歷首先訪問根結點然後遍歷左子樹,最後遍歷右子樹。在遍歷左、右子樹時,仍然先訪問
根結點,然後遍歷左子樹,最後遍歷右子樹。
(1)訪問根結點。
(2)前序遍歷左子樹。
(3)前序遍歷右子樹 。
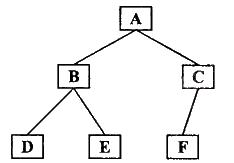 前序遍歷
前序遍歷需要注意的是:遍歷左右子樹時仍然採用前序遍歷方法。
前序遍歷結果:ABDECF
已知後序遍歷和中序遍歷,就能確定前序遍歷。
數學表達式形式
當對一棵數學表達式樹進行中序,前序和後序遍歷時,就分別得到表達式的中綴、前綴和後綴形式。
在後綴(postfix)表達式中,每個操作符跟在運算元之後,運算元按從左到右的順序出現。在前綴(prefix)表達式中,操作符位於運算元之前。在前綴和後綴表達式中不會存在歧義。
因此,在前綴和後綴表達式中都不必採用括弧或優先權。從左到右或從右到左掃描表達式並採用運算元棧,可以很容易確定運算元和操作符的關係。若在掃描中遇到一個運算元,把它壓入堆疊,若遇到一個操作符,則將其與棧頂的運算元相匹配。把這些運算元推出棧,由操作符執行相應的計算,並將所得結果作為運算元壓入堆疊。
複雜性
設二叉樹中元素數目為n。這四種遍歷算法的空間複雜性均為O (n),時間複雜性為O(n)。
當t 的高度為n時(右斜二叉樹的情況),通過觀察其前序、中序和後序遍歷時所使用的遞歸棧空間即可得到上述結論。
程式實現
C語言
樹節點結構和算法:
typedef struct TreeNode{ int data; TreeNode * left; TreeNode * right; TreeNode * parent;}TreeNode;void pre_order(TreeNode * Node){ if(Node != NULL) { printf("%d ", Node->data); pre_order(Node->left); pre_order(Node->right); }}調用時:
pre_order(Root); //Root為樹的根
Pascal版本
核心代碼:
procedure first(i:longint);
begin
write(a[i]);
if a[i*2]<>0 then first(i*2);
if a[i*2+1]<>0 then first(i*2+1);
end;
Java版本
二叉樹定義
publicclassTreeNode{ intval; TreeNodeleft; TreeNoderight; TreeNode(intx){ val=x; }}遞歸實現
publicvoidpreOrder(TreeNodebiTree){ System.out.printf(biTree.val+""); TreeNodeleftTree=biTree.left; if(leftTree!=null){ preOrder(leftTree); } TreeNoderightTree=biTree.right; if(rightTree!=null){ preOrder(rightTree); }}非遞歸實現
publicvoidpreOrder(TreeNodebiTree){ Stack<TreeNode>stack=newStack<TreeNode>(); while(biTree!=null||!stack.isEmpty()){ while(node!=null){ System.out.print(biTree.value+","); stack.push(biTree); biTree=biTree.left; } if(!stack.isEmpty()){ biTree=stack.pop(); biTree=biTree.right; } }} 前序遍歷
前序遍歷
