二叉鍊表是樹的二叉鍊表實現方式。
基本介紹
- 中文名:二叉鍊表
- 別稱:左孩子右兄弟表示法
- 適用領域範圍:數據結構
- 存儲結構:二叉鍊表
簡介,結構描述,二叉鍊表的功能定義,
簡介
樹的二叉鍊表實現方式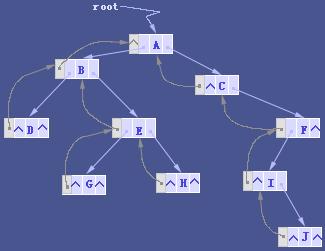

(孩子兄弟表示法)
以二叉鍊表作為樹的存儲結構。鍊表中結點的兩個鏈域分別指向該結點的第一個孩子結點和第二個孩子結點。
結構描述
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild , *netsibling;
} CSNode,* CSTree;
二叉鍊表的功能定義
bitree.h
//二叉鍊表定義
#include <iostream>
using namespace std;
typedef char TElemType;
struct BiTNode{
TElemType data;
BiTNode *lchild,*rchild;
};
typedef BiTNode *BiTree;
void initBiTree(BiTree &T);
void createBiTree(BiTree &T);
void preOrderTraverse1(BiTree T,void (*visit)(TElemType)); //非遞歸前序遍歷
void inOrderTraverse(BiTree T,void (*visit)(TElemType)); //遞歸中序遍歷
void levelOrderTraverse(BiTree T,void (*visit)(TElemType)); //層序遍歷
bitree.cpp
#include "bitree.h"
void initBiTree(BiTree &T){ //構造空二叉樹T
T=NULL;
}
void createBiTree(BiTree &T){
//按先序次序輸入二叉樹中結點的值('#'表示空格),構造二叉鍊表表示的二叉樹T。
TElemType ch;
cin>>ch;
if(ch=='#') // 空
T=NULL;
else{
T=new BiTNode;
if(!T)
exit(1);
T->data=ch; // 生成根結點
createBiTree(T->lchild); // 構造左子樹
createBiTree(T->rchild); // 構造右子樹
}
}
void preOrderTraverse(BiTree T,void (*visit)(TElemType)){
if(T){ // T不空
visit(T->data); // 先訪問根結點
preOrderTraverse(T->lchild,visit); // 再先序遍歷左子樹
preOrderTraverse(T->rchild,visit); // 最後先序遍歷右子樹
}
}
void preOrderTraverse1(BiTree T,void (*visit)(TElemType)){
BiTree s[100];
int top=0; //top為棧頂指針
while((T!=NULL)||(top>0)){
while(T!=NULL){
visit(T->data);
s[top++]=T;
T=T->lchild;
}
T=s[--top];
T=T->rchild;
}
}
void inOrderTraverse(BiTree T,void (*visit)(TElemType)){
if(T){
inOrderTraverse(T->lchild,visit); // 先中序遍歷左子樹
visit(T->data); // 再訪問根結點
inOrderTraverse(T->rchild,visit); // 最後中序遍歷右子樹
}
}
void postOrderTraverse(BiTree T,void (*visit)(TElemType)){
if(T){
inOrderTraverse(T->lchild,visit); // 後序遍歷左子樹
inOrderTraverse(T->rchild,visit); // 再後序遍歷右子樹
visit(T->data); // 最後訪問根結點
}
}
void levelOrderTraverse(BiTree T,void (*visit)(TElemType)){
