線索二叉樹

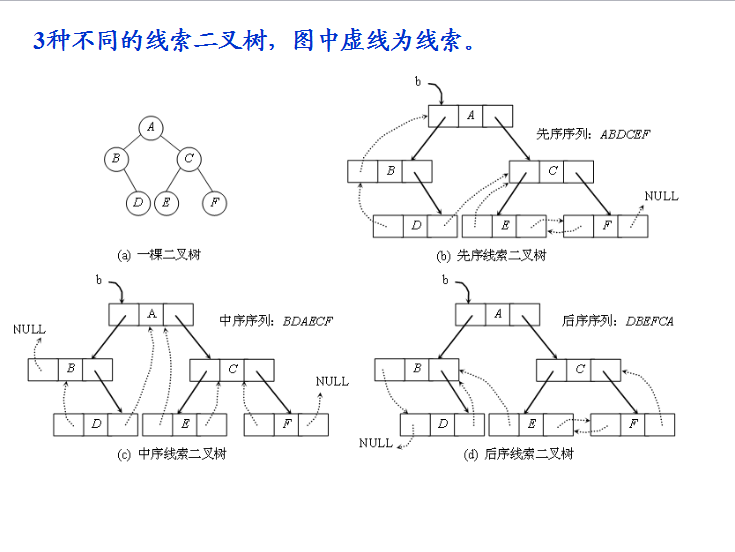
在二叉樹的結點上加上線索的二叉樹稱為線索二叉樹，對二叉樹以某種遍歷方式（如先序中序、後序）使其變為線索二叉樹的過程稱為對二叉樹進行線索化。

基本介紹

• 中文名：線索二叉樹
• 外文名：Threaded BinaryTree
• 領域：計算機科學

概念

對於n個結點的二叉樹，在二叉鏈存儲結構中有n+1個空鏈域，利用這些空鏈域存放在某種遍歷次序下該結點的前驅結點和後繼結點的指針，這些指針稱為線索，加上線索的二叉樹稱為線索二叉樹。

這種加上了線索的二叉鍊表稱為線索鍊表，相應的二叉樹稱為線索二叉樹(Threaded BinaryTree)。根據線索性質的不同，線索二叉樹可分為前序線索二叉樹、中序線索二叉樹和後序線索二叉樹三種。

注意：線索鍊表解決了無法直接找到該結點在某種遍歷序列中的前驅和後繼結點的問題，解決了二叉鍊表找左、右孩子困難的問題。

本質

二叉樹的遍曆本質上是將一個複雜的非線性結構轉換為線性結構，使每個結點都有了唯一前驅和後繼（第一個結點無前驅，最後一個結點無後繼）。對於二叉樹的一個結點，查找其左右子女是方便的，其前驅後繼只有在遍歷中得到。為了容易找到前驅和後繼，有兩種方法。一是在結點結構中增加向前和向後的指針，這種方法增加了存儲開銷，不可取；二是利用二叉樹的空鏈指針。

優勢與不足

優勢

(1)利用線索二叉樹進行中序遍歷時，不必採用堆疊處理，速度較一般二叉樹的遍歷速度快，且節約存儲空間。

(2)任意一個結點都能直接找到它的前驅和後繼結點。

不足

(1)結點的插入和刪除麻煩，且速度也較慢。

(2)線索子樹不能共用。

存儲結構

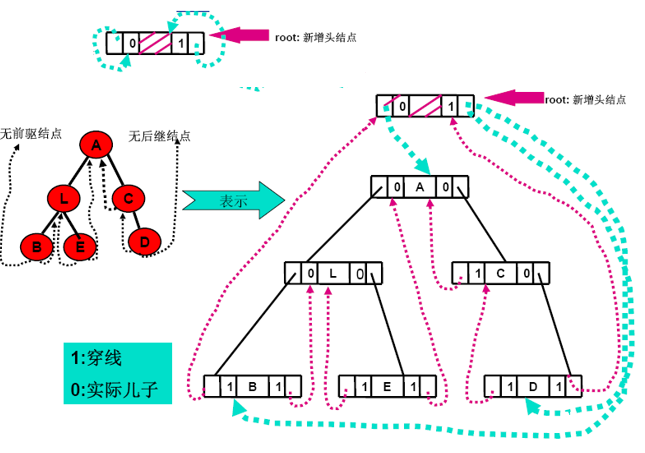
線索二叉樹中的線索能記錄每個結點前驅和後繼信息。為了區別線索指針和孩子指針，在每個結點中設定兩個標誌ltag和rtag。

當tag和rtag為0時，leftChild和rightChild分別是指向左孩子和右孩子的指針；否則，leftChild是指向結點前驅的線索(pre)，rightChild是指向結點的後繼線索(suc)。由於標誌只占用一個二進位，每個結點所需要的存儲空間節省很多。

現將二叉樹的結點結構重新定義如下：

lchild

ltag

data

rtag

rchild

其中：ltag=0 時lchild指向左兒子；ltag=1 時lchild指向前驅；rtag=0 時rchild指向右兒子；rtag=1 時rchild指向後繼。

構建

建立線索二叉樹，或者說對二叉樹線索化，實質上就是遍歷一棵二叉樹。在遍歷過程中，訪問結點的操作是檢查當前的左，右指針域是否為空，將它們改為指向前驅結點或後續結點的線索。為實現這一過程，設指針pre始終指向剛剛訪問的結點，即若指針p指向當前結點，則pre指向它的前驅，以便設線索。

另外，在對一顆二叉樹加線索時，必須首先申請一個頭結點，建立頭結點與二叉樹的根結點的指向關係，對二叉樹線索化後，還需建立最後一個結點與頭結點之間的線索。

下面是建立中序二叉樹的遞歸算法，其中pre為全局變數。

void InThreading(BiThrTree*p);//預先聲明BiThrNodeType*pre;BiThrTree*InOrderThr(BiThrTree*T){/*中序遍歷二叉樹T，並將其中序線索化，pre為全局變數*/BiThrTree*head;//線索二叉樹的頭結點，指向根結點head=(BitThrNodeType*)malloc（sizeof（BitThrNodeType））;/*設申請頭結點成功*/head->ltag=0;head->rtag=1;/*建立頭結點*/head->rchild=head;/*右指針回指*/if(!T)head->lchild=head;/*若二叉樹為空，則左指針回指*/else{head->lchild=T;pre=head;InThreading(T);/*中序遍歷進行中序線索化*/pre->rchild=head;pre->rtag=1;/*最後一個結點線索化*/head->rchild=pre;}returnhead;}voidInThreading(BiThrTree*p){/*通過中序遍歷進行中序線索化*/if(p){InThreading(p->lchild);/*左子樹線索化，遞歸*/if(p->lchild==NULL)/*前驅線索*/{　p->ltag=1;p->lchild=pre;}elsep->ltag=0;if(p->rchild==NULL)p->rtag=1;/*後驅線索*/elsep->rtag=0;if(pre!=NULL&&pre->rtag==1)pre->rchild=p;pre=p;InThreading(p->rchild);/*右子樹線索化*/}}

進行中序線索化的算法：

bithptr*pre=NULL;/*全程變數*/voidINTHREAD(bithptr*p){if(p!=NULL){if(p->ltag==0)INTHREAD(p->lchild);/*左子樹線索化*/if(p->lchild==NULL){p->ltag=1;p->lchild=pre;}if(p->rchild==NULL)p->rtag=1;if(pre!=NULL&&pre->rtag==1)pre->rchild=p;pre=p;/*前驅指向當前結點*/if(p->rtag==0)INTHREAD(p->rchild);/*右子樹線索化*/}}

線索二叉樹查找前驅和後繼：

（1）中序線索二叉樹：若結點的ltag=1，lchild指向其前驅；否則，該結點的前驅是以該結點為根的左子樹上按中序遍歷的最後一個結點。若rtag=1，rchild指向其後繼；否則，該結點的後繼是以該結點為根的右子樹上按中序遍歷的第一個結點。

求後繼的算法如下：

bithptr*INORDERNEXT(bithptr*p){if(p->rtag==1)return(p->rchild);else{q=p->rchild;/*找右子樹最先訪問的結點*/while(q->ltag==0)q=q->lchild;return(q);}}

求前驅的算法如下：

bithptr*INORDERNEXT(bithptr*p){if(p->ltag==1)return(p->lchild);else{q=p->lchild;/*找左子樹最後訪問的結點*/while(q->rtag==0)q=q->rchild;return(q);}}

（2） 後序線索二叉樹：

在後序線索二叉樹中查找結點*p的前驅：若結點*p無左子樹，則p->lchild指向其前驅；否則，若結點*p有左子樹，當其右子樹為空時，其左子樹的根（即p->lrchild）為其後序前驅。當其右子樹非空時，其右子樹的根（即p->rchild）為其後序前驅。

在後序線索二叉樹中查找結點*p的後繼：若結點*p為根，則無後繼；若結點*p為其雙親的右孩子，則其後繼為其雙親；若結點*p為其雙親的左孩子，且雙親無右子女，則其後繼為其雙親；若結點*p為其雙親的左孩子，且雙親有右子女，則結點*p的後繼是其雙親的右子樹中按後序遍歷的第一個結點。所以，求後序線索二叉樹中結點的後繼要知道其雙親的信息，要使用棧，所以說後序線索二叉樹是不完善的。

（3）先序線索二叉樹：

在先序線索二叉樹中查找結點的後繼較容易，而查找前驅要知道其雙親的信息，要使用棧，所以說先序線索二叉樹也是不完善的。