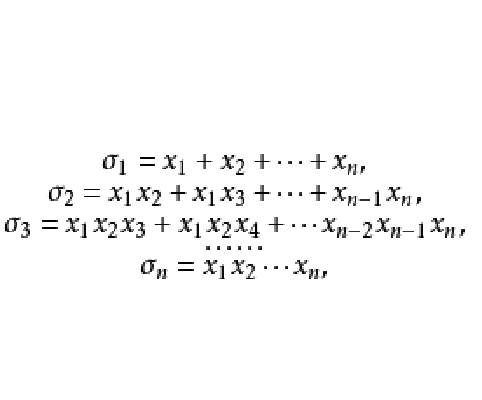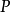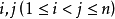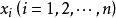初等對稱多項式

n個關於變數x₁，x₂，…，x_n的多項式：p₁=x₁+x₂+…+x_n，p₂=x₁x₂+x₁x₃+…+x_n-1x_n，……p_n=x₁x₂…x_n叫做初等對稱多項式(elementary symmetric polynomial)，或叫做基本對稱多項式，任何對稱多項式都可以表示成初等對稱多項式。

基本介紹

• 中文名：初等對稱多項式
• 外文名：elementary symmetric polynomial
• 別名：基本對稱多項式
• 所屬學科：數學
• 相關概念：多項式、對稱多項式等

定義

設 為數域 上的 元多項式，如果任意交換兩個文字，多項式均不變，即對任意 都有

則稱 為數域P上的一個n元對稱多項式。下列n個對稱多項式

稱為初等對稱多項式。

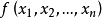
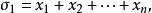
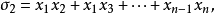
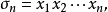
有關結論

(1) 對稱多項式的和、乘積仍是對稱多項式；對稱多項式的多項式仍是對稱多項式。

(2) 對稱多項式基本定理 設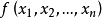 為數域P上的一個n元對稱多項式，則存在惟一的n元多項式 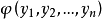，使得， ，其中 為初等對稱多項式。

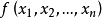
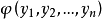
將對稱多項式表示為初等對稱多項式

下面介紹兩種將對稱多項式表為初等對稱多項式的多項式的方法。

方法1

逐步消去首項法

這是推導對稱多項式基本定理時給出的方法，其一般步驟是：

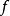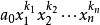第一步 首先找出對稱多項式 的首項 ，則一定有

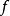
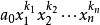
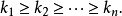
第二步 由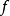 的首項寫出 。

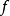
第三步 作 ，並展開化簡。

再對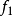 按第一、二、三步進行，構造 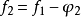，如此反覆進行，直至出現 ，則

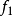
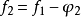
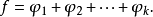
方法2

待定係數法

設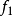 是m次齊次對稱多項式，用待定係數法求解的一般步驟是：

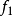
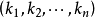第一步 根據 的首項指標組寫出所有可能的指標組 ，這些指標組應滿足① 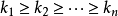；② ；③前面的指標組先於後面的指標組。

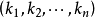
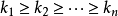
第二步 由指標組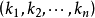 寫出對應的初等對稱多項式的方冪的乘積

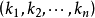
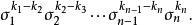
第三步 設出 由所有初等對稱多項式的方冪乘積的線性表達式，其首項係數即為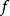 的首項係數，其餘各項係數分別用 代替。

第四步 分組選取適當的 的值，計算 及 ，代人第三步中設出的表達式得到關於 的線性方程組，解這個線性方程組求得 的值，最後寫出所求的 的表達式。

注意：① 當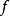 是非齊次對稱多項式時，可以將它表成若干齊次對稱多項式的和，把它的每一個齊次對稱多項式表為初等對稱多項式的多項式，再把所得到的各部分相加即可。

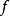
② 待定係數法是深入研究對稱多項式基本定理的證明過程而得出的簡化方法，要求熟練掌握。