分類空間是在纖維叢理論中起關鍵作用的一類空間。任意拓撲群 G 的分類空間總是存在的。分類空間的確切含義由分類定理得到體現。
基本介紹
- 中文名:分類空間
- 外文名:classifying space
- 適用範圍:數理科學
定義



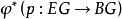
拓撲群的分類空間
分類定理


分類空間是在纖維叢理論中起關鍵作用的一類空間。任意拓撲群 G 的分類空間總是存在的。分類空間的確切含義由分類定理得到體現。



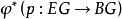

分類空間是在纖維叢理論中起關鍵作用的一類空間。任意拓撲群 G 的分類空間總是存在的。分類空間的確切含義由分類定理得到體現。...
定義空間因為人口、種族、經濟、文化、環境特徵而劃分類型區。也用在地理信息系統圖像圖形分析中作為圖形代數的運算單元。 ...
建築空間是人們為了滿足人們生產或生活的需要,運用各種建築主要要素與形式所構成的內部空間與外部空間的統稱。它包括牆、地面、屋頂、門窗等圍成建築的內部空間,以及...
空間分析是對於地理空間現象的定量研究,其常規能力是操縱空間數據使之成為不同的形式,並且提取其潛在的信息。空間分析是GIS的核心。空間分析能力(特別是對空間隱含...
《D類空間》是一款策略小遊戲,遊戲目標是征服銀河。...... 分類藝術 科學 自然 文化 地理 生活 社會 人物 ...《D類空間》是一款策略小遊戲,遊戲目標是征服銀河...
空間尺度一般是指開展研究所採用的空間大小的量度。按面積分為部分地區、局部地區和大部地區,按緯度分為副熱帶或亞熱帶。空間尺度在建築學領域又有不同的意思,...
所謂有限空間,是指封閉或者部分封閉,與外界相對隔離,出入口較為狹窄,作業人員不能長時間在內工作,自然通風不良,易造成有毒有害、易燃易爆物質積聚或者氧含量不足...
存儲器是計算機系統的重要資源之一,計算機系統的存儲器分為兩類:主存和輔助存儲器。空間分配是指對主存和輔助存儲器空間的分配。主存和外存空間分配很多相同之處:...
空間概念(space concept)是指人腦對物體在空間內的存在形式產生的間接的、概括的反映。涉及形狀、大小、遠近、深度、方位等。在空間知覺的基礎上建立起來的,是對...
網站空間英文名:WebSite host。簡單地講,就是存放網站內容的空間。網站空間也稱為虛擬主機空間,通常企業做網站都不會自己架伺服器,而是選擇以虛擬主機空間做為放置...
空間數據又稱幾何數據,它用來表示物體的位置、形態、大小分布等各方面的信息,是對現世界中存在的具有定位意義的事物和現象的定量描述。根據在計算機系統中對地圖是對...
空間技術,是探索、開發和利用太空以及地球以外天體的綜合性工程技術,亦稱航天技術。1957年10月4日,蘇聯成功發射了世界上第一顆人造地球衛星,標誌著人類跨入了航天...
空間維度,是地理現象的最基本特徵。它是根據地理對象的實際分布特徵以及地圖表達的需要來確定的,包括:0維、1維、2維、2.5維和3維。空間維有兩種。可能很大延伸得...
形態除了空間本質屬性外,還有多樣性、可感性、變通性等不同屬性,對於“形態”這一詞的複雜化理解可衍生出多個交叉學科。當被賦予“空間”修辭時,其形態歸屬被類別...
分類藝術 科學 自然 文化 地理 生活 社會 人物 經濟 體育 歷史...空間區域主角 編輯 姓名:葉月月(葉天)介紹:從平行世界穿越過來的葉天附身上本...
“維”是一種度量,在三維空間坐標上,加上時間,時空互相聯繫,就構成四維空間。現在科學家的理論認為整個宇宙是十一維的,只是人類的理解只能理解到3維,打個比喻:一...
居住空間(habitable space)系指臥室、起居室(廳)的使用空間。對於居住者而言,居住空間不僅是一種功能,更是集裝飾與實用於一體。居住空間,就是個性的詮釋。臥室、...
SI(Space Identity)稱為空間識別,也叫做(store Identity),或Interior Identity(室內識別),也可以把它當作VI的延伸,但主要目的是在“三維空間”,“裝潢規格化”作業...
空間分布指水生生物在水域空間的分布。...... 分類藝術 科學 自然 文化 地理 生活 社會 人物 經濟 ...空間分布指水生生物在水域空間的分布。中文名稱 空間分布 ...
解空間是指齊次線性方程組所有解的集合構成一個向量空間。...... 分類藝術 科學 自然 文化 地理 生活 社會 人物...解空間是指齊次線性方程組所有解的集合構成一個...
“巴納赫空間”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
空間規劃體系是以空間資源的合理保護和有效利用為核心,從空間資源(土地、海洋、生態等)保護、空間要素統籌、空間結構最佳化、空間效率提升、空間權利公平等方面為突破,...
空間信息是反映地理實體空間分布特徵的信息。空間分布特徵包括實體的位置、形狀及實體間的空間關係、區域空間結構等。...
空間關係是指各實體空間之間的關係,包括拓撲空間關係,順序空間關係和度量空間關係。由於拓撲空間關係對GIS查詢和分析具有重要意義,在 GIS中,空間關係一般指拓撲空間...
空間位置數據描述地物所在位置,這種位置既可以根據大地參照系定義,為了精確描述物體的空間位置,物理學中,通常藉助數學方法,建立坐標系來描述物體的位置。...
指在部落格(Blog或Weblog)的虛擬空間中發布文章等各種形式的過程。...可以簡單地從日誌內容,部落格界面,文章數量,日誌分類,人氣指數,體現出博主的個性...
