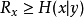分散式信源編碼

介紹

分散式信源編碼的主要套用領域有感測器網路(sensor network)和圖像,視頻,多媒體壓縮. 其最主要的特點有兩條,第一, 編碼計算非常簡單, 解碼相對比較複雜; 第二, 互不通信的信息相關的信源壓縮可以達到有互相通信的壓縮效率.

理論值

做為資訊理論的一個分支, 早在1973年David Slepian和Jack K. Wolf就利用信息熵提出針對於兩個信息互相關聯信源無損壓縮的理論極限, 稱之為斯理篇-伍夫界限(Slepian-Wolf bound). 他們證明了兩個互不通信的信息相關的信源壓縮可以達到有互相通信的壓縮效率. 這個壓縮界限後來被Thomas Cover擴展到了多個相關信源的情況.

於1976年, A. Wyner和J. Ziv在考慮高斯信源的有損壓縮時得到了類似的結果. Wyner-Ziv界限在解碼誤碼率為零時等於Slepian-Wolf界限.

歷史

2003年, Pradhan和Ramachandran把校驗子(syndrome)運用到了分散式信源網路並稱之為DIstributed Source Coding Using Syndromes (DISCUS). 他們將兩個二進制的信源分成定長的組,對於一個信源用定長碼壓縮得到這些組的校驗子, 而另外一個信源則完全不壓縮,作為邊信息. 這種碼率不均衡的分散式信源編碼壓縮方式成為不對稱壓縮(asymmetric DSC). 顯而易見的是,反覆使用前一個信源的信息作為邊信息, 這種不對稱的壓縮方式可以輕易的擴展到多個信源. 有些分散式信源編碼系統使用的奇偶校驗子(parity-check bits).

在先今的分散式信源編碼中, 常常用虛擬信道作為兩個相關信源的關聯性的模型, 二元對稱信道Binary symmetric channel多用於描述虛擬信道的特性.

在對兩個相關聯的信源的相關性研究中, 通常用到兩種模型: 確定式和機率式. 基於這兩種模型, 分散式信源編碼被擴展到跟普遍性的方式:兩個信源都被壓縮, 不存在所謂的邊信息. 這種更普遍的方式被稱為非不對稱壓縮(Non-asymmetric DSC).

基於一種確定式的虛擬信道模型,X. 曹和M. Kuijper將非不對稱壓縮的分散式信源編碼擴展到任何數量的相關信源, 每個信源可以更靈活的在Slepian-Wolf界限內達到任意壓縮碼率, 而所有信源壓縮後的總碼率和不對稱式多信源的總碼率相同 .