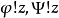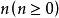分支類型論

分支類型論(ramified theory of types)亦稱“分枝類型論”、“類型支論”，是英國哲學家、邏輯學家羅素為了使數學的邏輯主義構造能避免出現悖論而發展起來的理論。按照這一理論，首先應對集合(謂詞)進行分類(Type)：屬於0類的是個體(即給定的不作邏輯分析的東西)，屬於1類的是個體的集合，屬於2類的是1類中的集合的集合，也即個體的集合的集合，…,。類的劃分的原則是：任何集合都必須從屬於確定的類，另外，對命題的組成來說，則只有“某一類對象是否屬於僅次於它的那一類的集合”這樣的表達式才是有意義的。在分支類型論中，還必須按照定義的方式對同一類中的集合進行級(Order)的劃分：一般地說，那些在定義中沒有涉及到所有集合的集合是第1級的，而那些在定義中涉及到“第n級的所有集合”的集合則是第(n+1)級的。級的劃分原則是每一集合都屬於一定的級；而且，如果不具體地說明所討論的(類和)級，那種涉及到“所有集合”的表達式就是無意義的。

由於級的劃分是在類中進行的，因此，上述理論就稱為分支類型論。一般認為，如果嚴格實行分支類型論的要求的話，所有已知的悖論就可以得到避免，但這同時也給數學理論的展開帶來了嚴重的困難。

基本介紹

• 中文名：分支類型論
• 外文名：ramified theory of types
• 所屬學科：邏輯學
• 別名：“分枝類型論”、“類型支論”
• 提出者：羅素

基本介紹

分支類型論把類不僅劃分成型，而且還劃分成階(亦稱級)的類型論。英國羅素於1908年在《以類型論為基礎的數理邏輯》一文中首次提出這一理論，並在《數學原理》(1910—1913)中對它作了系統的表述。羅素持“無類理論”的立場，他不是從類出發、而是從命題函式出發來構造分支類型論的。羅素對命題函式進行了嚴格的分層處理，最低層次的函式是個體，用字母表示個體變元，可稱為0階函式；比個體高一層次的是一階函式，它是以個體為自變元或約束變元的函式，例如等等；更高一個層次的是二階函式，它以個體和一階函式為變元(自變元或約束變元)，且變元中至少包含一個一階函式，例如，設為的一階函式，則等都是二階函式。一般的，如果一個函式中變元(自變元或約束變元)的最高階是，則稱這一函式是階的。羅素遵從“惡性循環原則”，把命題函式區分為直謂的和非直謂的。對什麼是直謂函式，他作了嚴格的定義：對一元函式而言，當函式的階恰比它的自變元的階高1時，稱為直謂的，一般的，對於有個自變元的k元命題函式，若k個自變元的最高的階為n，而函式的階為，則稱該k元函式是直謂的。由此可知，一階函式都是直謂函式，但二階和二階以上的函式則劃分為直謂與非直謂兩種。羅素進而引入可歸化公理：對任何命題函式，必存在一個與它形式等價的直謂函式。在這一公理和命題函式分層的基礎上建立起類的理論並發展了數學。由於羅素的分支類型論過於複雜，近代數理邏輯學家在介紹分支類型論時往往採用與羅素不同的更為簡潔的處理方式。這種處理方式以明確的類的觀點為出發點，從“型”與“階”(亦稱為級)兩個不同的方面進行分層。一方面按類進行外延的分層，即分為個體、個體的類或性質(謂詞)，個體的類的類或個體的性質(謂詞)的性質(謂詞)，……分別稱為0型，1型，2型，……;另一方面又對性質(謂詞)作階的劃分，在定義方法上未涉及所有性質(謂詞)的那些性質(謂詞)是一階的，它相當於直謂函式，下定義時僅涉及一階性質(謂詞)全體的那些性質(謂詞)稱為二階的，……一般的，下定義時最高涉及階性質(謂詞)全體的那些性質(謂詞)稱為階的，當階時，這一性質(謂詞)就相當於非直謂函式。分支類型論可避免一切已知的悖論，但是由於若不引入可歸化公理就無法推出數學，而可歸化公理的實際作用正是取消“階”(亦稱為級)的劃分而保留“型”的劃分，從而分支類型論就又將轉化為簡單類型論。

描述論分析

分支類型論是羅素所提出的一種解悖方案。羅素考察了其他悖論解決辦法，覺得這些方案都不能令人滿意。他認為“整個秘密的關鍵是邏輯類型的不同”，“自我指稱”是所有悖論的共同特徵，悖論就產生於一種惡性循環。這種惡性循環是定義其成員時要涉及集體的整體造成的。因此，只有消除惡性循環，才能避免悖論。正是根據“凡是涉及一個集體的整體的對象，它本身不能是該集體的成員”這樣一個原則，羅素提出了他的分支類型論。

羅素把論域分成類型，提出只有在這樣的情況下才能談到它們的全體：滿足某一給定條件的所有對象都屬於同一類型；因此一個類的所有成員必定全都具有同一類型。任何性質的分類都必須按照它所屬的對象類型：給定的、未作邏輯分析的原始客體或個體屬於第一層次類型，個體的性質屬於第二層次類型，個體的性質的性質屬於第三層次類型，以此類推。同時，對於基本類型以上的類型，還要給同一類型中的不同性質作出“級”的劃分：下定義時沒有提到任何總體性質的性質屬於第一級，下定義時用到某級性質的總體的性質屬於第二級，以此類推。由於任何性質都屬於一定的類型和級，而級是在類型之內劃分的，所以這種理論被叫作“分支類型論”。

根據“分支類型論”，如果我們作出這樣的規定，每一類型中的對象都不能以這一類型的整體及更高類型中的對象定義，每一類型的性質只有當用於它之下的那個類型的對象時才具有意義；而且，每一級的性質都不能以這一級性質的總體和更高的級中的性質定義，凡是只能藉助屬於第13級的“所有性質”來定義的第n+1級的性質，決不能包含在第n級的性質中，如果不能具體指明屬級，則涉及“所有性質”的表達式沒有意義。由此，我們就能在整個系統中排除悖論。

這種解決方法非常好，分支類型論的確由此排除了一些悖論，但問題是，在排除一些悖論的同時也把許多合理的東西排除在外了。特別是一些重要的數學定理因而不能被證明，而一些必要的數學概念的定義則變成非法的。而且，一方面，分支類型論的悖論消解只是一種形式上的解決，在哲學層面，這種解悖方案始終不能令人滿意；另一方面，分支類型論禁例太嚴，以致無法推出全部數學。因此，就RZH標準的“充分寬廣”來說，分支類型論也遇到嚴重困難。正如哈克指出的：

無論在形式的水平上，還是在哲學的水平上，羅素的理論都陷入了困難。在形式上，羅素的做法有“因噎廢食”的危險，他的限制避免了悖論卻也限制了某些必要的推論。

分支類型論對於解決集合論悖論有效，毫無疑問抓住了其規定(類的規定)的關鍵，從而在形式上富有成效地解決了集合論悖論的構成問題。但它作為哲學上解決方法的惡性循環原則卻沒有真正深入哲學層面。惡性循環仍然屬於悖論形成的邏輯形式方面的內容，它只是悖論而且是某些悖論形成的邏輯形式條件。違反這一原則並不一定導致悖論。而且被這一原則排除的循環並不一定是惡性的。因而羅素的解悖理論不是陷入形式上和哲學上的雙重困難，而是因為其哲學的解決方法的實際缺失必然導致形式上的解決方法因不徹底而不可避免地陷入困難。

羅素解悖方案的實質是富有成效地從形式的解決方法人手，止於哲學的解決方法。這樣必定導致其形式上的努力不受哲學基礎的范導，或者說缺少哲學大背景——大坐標的參照和定位而“惡性”蔓延，從而有與“因噎廢食”原則相悖的傾向。它所制定的限制在避免了悖論產生的同時，也限制了一些必要的推論。羅素將數學還原為邏輯的努力之所以沒有獲得最後成功，正是因為其類和級的限制不是建立在規定的相對性的基礎之上，沒有注意到類是級的規定，既與客體的屬性相關，也與主體的認識目的和實踐需要相關，因此與人類學特性相關，從而把類和級作了純客觀化的理解，形成了一種脫離主觀規定的絕對的限制，堵死了許多必定建立在相對規定基礎上的重要數學內容。

由於類型論起作用是因為類型的區分隔離了不同語言層次間規定發生衝突，只是一種形式上的處理，因而沒有理論支撐，只是一種描述限制。正如戈德斯坦指出的：

羅素和懷特海把他們的規則稱作“類型論”，但問題是這些規則後面根本沒有真正的理論，就像他們自己沮喪承認的那樣；對於為什麼某種集合被允許而其他的不被允許，除了說如果人們允許不可允許的集合，那么他的系統里將會發生非常糟糕的事情之外，沒有給出任何解釋。他們的形式系統是通過法令(fiat)達成一致的。

“惡性循環”原則不成立，由此建立起來的“分支類型論”也行不通。分支類型論解悖方案不能解決悖論問題，羅素本人因此最後成了一個不可知論者。他在晚年時感嘆道，“我所一直尋求的數學中的光輝的確定性，在令人困惑的迷宮中喪失了。”“尋求完美、最後定論和確定性的希望破滅了。”

作為一種形式上的解悖方案，分支類型論不僅因禁例太多而與數學不相協調，而且沒有能夠從哲學層面面對悖論問題。這一點，通過“理髮師定理”的漫畫式放大，將變得更為清楚。

20世紀60年代初，英國邏輯學家湯姆遜(J.F.Thomson)提出一條“定理”，試圖找到“集合論悖論”的統一解。另一位英國邏輯學家麥基(J.L.Mackie)對其進行研究後把它叫作“理髮師定理”。這條定理是這樣的：

設S是一個集合，R是一個關係，這個關係至少在S上有定義。則S中不存在這樣一個元素y，這個y僅僅同S中所有這樣一些元素有關係R：這些元素自己同自己無R關係。

用“理髮師定理”消解“理髮師悖論”很簡單。在所有薩爾維村的村民這個集合中，任取兩個村民x，y，這兩個村民可以是同一個人，那么，“x給y刮鬍子”不是真的就是假的，即是說，這表明“……給……刮鬍子”這個二元關係至少在該集合上有定義。由“理髮師定理”可知，在薩爾維村的村民中根本不存在這樣的理髮師，他給且只給所有不給自己刮鬍子的人刮鬍子。這樣一個“搗亂”的理髮師根本就不存在，也就意味著根本不存在什麼理髮師悖論。

用“理髮師定理”消解“目錄障論”也很簡單。

“目錄障論”是“羅素悖論”的又一個通俗“版本”，由瑞士數學家貢賽斯(Gonseth)提出。我們可以把所有可能的目錄分為兩大類：一類是不把自身收入在內的目錄，一類則是把自身收入在內的目錄。所有不把自身收入在內的目錄構成一個總目錄，這個總目錄本身也是目錄。既然它也是目錄，便有個是否把自身收入在內的問題。這樣，悖理性就產生了：如果該總目錄不把自身收入在內，它便把自身收入在內；如果它不把自身收人在內，則又把自身收入在內。

在目錄悖論中，從所有可能的目錄構成的集合中，任取兩個目錄x，y，這兩個目錄可以是相同的，則“x收入y”不是真的就是假的。即“……收入……”這個二元關係至少在該集合上有定義。由“理髮師定理”可知，根本就不存在這樣一個目錄，它收入且僅收入所有那些不把自身收入在內的目錄。這樣一個“麻煩”的目錄根本就不存在，也就意味著根本就不存在什麼目錄悖論。

也就是說，像羅素所說的“理髮師”即使存在，也不在形式邏輯能解釋和接受的範圍。形式邏輯只能把悖論一筆抹除。

“理髮師定理”是一條“局限性定理”，它企圖證明邏輯悖論具有“局限性”。儘管人們認為事實上這只是證明了形式邏輯本身的局限性，但這條定理在消解悖論上有一定作用。根據“理髮師定理”，湯姆遜解釋了理髮師悖論、形容詞悖論、羅素悖論和理察悖論。據湯姆遜論證，這些悖論都能變成“定理”，有的還可以算作數學定理。他認為羅素的“類型論”和塔爾斯基的“語言層次論”等規避悖論的方法，實質上與這個方法大同小異，而這個定理則更簡潔。

在“理髮師定理”發表十多年後，有人提出了異議。麥克伊(J.L.Mackie)就對它作了這樣的評論：

這種證明解除了悖論嗎?顯然沒有。它擺脫了理髮師……但它不能擺脫羅素悖論或格雷林悖論，因為我們手上仍然有一個矛盾存在：一方面是“理髮師定理”的適當解釋；另一方面則顯而易見地存在著不包含自身為元素的集合……這一個矛盾(“羅素集”是又不是自身的元素)，靠了否認這樣的集合的存在而被解除，但一個更深刻的矛盾仍然存在：即否認這個集合的存在和這個集合的顯然存在之間的矛盾。湯姆遜的解除方法自身成為這個更深的矛盾中的一方。

而且，“理髮師定理”也不能直接用於“說謊者悖論”的解決。“理髮師定理”像是“湯姆遜剃刀”，可以消解“理髮師悖論”和“目錄悖論”，但這把“剃刀”對“羅素悖論”卻無能為力。

“理髮師定理”的實質的確就是：不但“矛盾即荒謬”，而且“矛盾不存在”。湯姆遜的做法，事實上是一種把悖論變成規定的做法。的確，規定有時候可以是“蠻橫”、“不講理的”，但規定至少有個是否合理的問題。“理髮師定理”之所以只能擺脫“理髮師”而不能擺脫“羅素集”，就因為“理髮師”是經驗的而羅素集是邏輯的。經驗的東西可以存在也可以不存在，而邏輯的東西是否存在是有其邏輯必然的。

“理髮師定理”本身是新作出的一個規定。用“理髮師定理”去消解“理髮師悖論”和“目錄悖論”，無非就是通過運用這個規定，將“只給所有不給自己刮鬍子的人刮鬍子的理髮師”和“收入且僅收人所有那些不把自身收入在內的目錄”給否定了。這裡與其說是消解悖論，不如說在閹割悖論，把悖論變成了一般命題，把公雞變成了閹雞。這樣消解理髮師悖論和目錄悖論當然是再容易不過了。“理髮師定理”之所以不能用於消解羅素悖論，是因為這兩個悖論所涉及的是有限集合，而羅素悖論涉及大全集，即所有集合的集合。而大全集並不存在。因此用“理髮師定理”並不能否定“羅素集”的存在。正因為這個“定理”僅局限在理髮師悖論和目錄悖論的消解，所以英國邏輯學家麥基(J.L.Mackie)把它稱作“理髮師定理”的確是不無貶義的。其實，即使我們能夠通過“理髮師定理”否定“羅素集”的存在，也不能完全解決羅素悖論，這樣做也更不是在有效解決悖論問題。

當我們進一步深入描述的深層就會看到，事實上，簡單地否定“給且只給不給自己刮鬍子的人刮鬍子的理髮師”、“不收入自身的目錄的總目錄”和“羅素集”，只是對悖論的消極的消解，並沒有真正進入悖論的殿堂。因為從描述的角度看，這些在相應的描述中都是一些有意義的規定。在描述中，這些規定的存在是可以有不同層次含義的，不能簡單地予以否定，即使“最大的自然數”這樣的規定，也是不能簡單地否定其存在及其意義的。與其說“最大的自然數是不存在的”，不如說我們不能寫出一個最大的自然數。由此，我們也可以看到“最大的自然數”的描述意義。

通過否定“給且只給不給自己刮鬍子的人刮鬍子的理髮師”、“收入且僅收入所有那些不把自身收入在內的目錄”乃至“羅素集”的存在消解悖論，只是對悖論的頭痛醫頭腳痛醫腳式處理，沒有深人悖論問題的深層。只有不斷深入描述的深層，我們才可能把悖論問題的研究真正引向深入，而這已經是從描述人手探索悖論問題的開始。

從描述人手，類如“理髮師”那樣的概念從讓人們左右為難的“怪物”變成了人類描述和認識中的一個新的梯階；從而處理這些概念也不再是迴避一個無從下手的難題。這樣一來，“理髮師定理”不再是一個無效排除“理髮師”存在的規定，而是從一個層面向另一個更高層面過渡的界碑，人類描述(和規定)系統中分類的新依據。

“理髮師定理”事實上是一把閹刀，其運用就是用規定閹割悖論。用規定來否定一個現象的存在，終究類似掩耳盜鈴或鴕鳥行為，這樣是迴避不了悖論的。事實上，如果把“理髮師定理”那樣的東西看作規定，並進一步把這一規定的地位弄清楚，我們就會發現這是我們描述中的正常現象。只要我們不是把這些規定作為閹割悖論的閹刀，而是把它作為描述的界標，我們就能意識到人類描述的特殊處境。而從這一特殊處境我們可以看到，正是這些規定把人類描述推向一個個新的更高層面。

正是由於沒有把“理髮師”等作為整個描述和規定系統中的一個新界標，羅素的類型論未能解決而只是迴避了集合論悖論，誠如楊熙齡先生談到用類型論解決目錄悖論時所指出的：

那么，羅素的“類型論”能否幫助卡里馬楚斯擺脫困境呢?能，但是那等於是建議卡里馬楚斯不要編這種目錄，連那第一大類：“自身列入的目錄的總目”也不要編，甚至連“自身列入的目錄”也不要編。因為按照“類型論”的原則是：“一個集合不能是這個集合本身的元素；集合不準包含它自身在內。”如果要說甲屬於乙，乙必須在“類型”上比甲高一級。因此，如果有一部目錄包含它自己的名目，即違反“類型論”規則，而成為“無意義”。這樣當然再不會出現一部目錄列入不列入自身的問題。

那么卡里馬楚斯雖然擺脫了困境，可是也就無事可做了。卡里馬楚斯將會陷入新的困惑境地；毛病出在哪兒，是出在這種區分法上?兩大類一分開之後，倒弄得不可分了?……

同羅素的“類型論”相比，許多悖論的推理倒顯得很自然、很合理。

規定不準有這樣一部“總目”，只顯得這種規定自身的無力。目錄可以有列入自身者，這是客觀的事實，而羅素的“類型論”強加禁止。既有“列入自身”者，當然也會出現“不列入自身”者。這是符合“矛盾律”的，“矛盾律”要求這樣劃分。那么可以說後來的矛盾竟是因為執行了“矛盾律”才產生的，可是“矛盾律”又不允許這部“總目”既被列入又不被列入自身，“排中律”還規定要么列入自身，要么不列入自身，兩者必居其一。這仿佛“矛盾律”和“排中律”在挑它們自己的刺兒。

其實，不僅羅素，理察也採用了類似的解悖辦法。在發表以他命名的悖論的同時，理察也提出了他的解悖辦法：避免一個集合中包含這樣的元素，這個元素本身需要藉助於這個集合來定義。理察認為，只要不允許藉助於一個總體來定義一個對象，而該對象本身又屬於這一總體的情況存在，就能避免理察悖論和其他悖論。這是一些典型的對悖論的形式化解決辦法，只停留於對悖論問題的消極而不徹底的解決。

當一個描述超出或套用於作為其前提的規定時，描述會失去意義。這並不是描述或規定本身不合理，而是超出了原來的描述範圍，必須有新的規定才能推進描述的發展。如果只停留於原先的描述框架，就會陷於悖理性，正像如果沒有新的觀念(規定、定律等)，相對論現象只能停留在牛頓力學描述框架中，以一種悖理性的方式存在。