數理邏輯中遞歸論的一部分。它的中心論題是用遞歸論為工具給出數集(問題集)或函式集的複雜性的某種排序。
基本介紹
- 中文名:分層理論
- 釋義:數理邏輯中遞歸論的一部分
- 實質:理論
- 詳細內容:見正文
簡介
詳解
這樣,一謂詞是算術的即是可表成下列形式之一:,其中為一般遞歸謂詞,同時,根據量詞的個數及公式最外邊的量詞是扽 還是凬而分別記成型或型(型的對偶形式)。例如,形如 扽的謂詞全體記作,而形如凬扽的謂詞全體則記作。
把可以用兩種形式及來表示的謂詞全體記作。
例如,易見(此即把遞歸集定義作最簡單的算術集)。
又如,(此即一謂詞屬於的充要條件為它是一般遞歸的)。
在≥1的情形,恆存在一個枚舉類(或)的全體謂詞的枚舉謂詞。例如,對於和m==1而言,存在一個原始遞歸謂詞(,,,,),使得當任給一個一般遞歸謂詞(,,,)時,恆有自然數,使得
此即枚舉定理。在這個定理中,可將(,,,,)取為屶(,,,)則有分層定理。
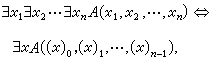 分層理論
分層理論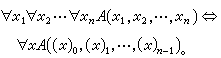 分層理論
分層理論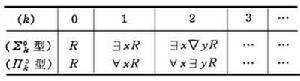 分層理論
分層理論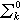 分層理論
分層理論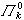 分層理論
分層理論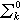 分層理論
分層理論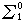 分層理論
分層理論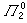 分層理論
分層理論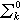 分層理論
分層理論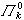 分層理論
分層理論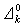 分層理論
分層理論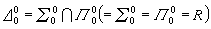 分層理論
分層理論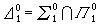 分層理論
分層理論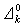 分層理論
分層理論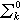 分層理論
分層理論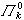 分層理論
分層理論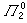 分層理論
分層理論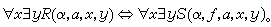 分層理論
分層理論分層定理
所以,這就得到了一個方便的分層(1)來給算術謂詞(算術集)分類。這個分層稱為算術分層。
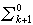 分層理論
分層理論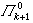 分層理論
分層理論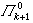 分層理論
分層理論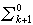 分層理論
分層理論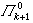 分層理論
分層理論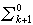 分層理論
分層理論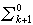 分層理論
分層理論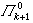 分層理論
分層理論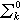 分層理論
分層理論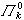 分層理論
分層理論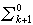 分層理論
分層理論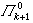 分層理論
分層理論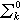 分層理論
分層理論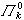 分層理論
分層理論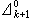 分層理論
分層理論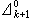 分層理論
分層理論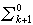 分層理論
分層理論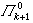 分層理論
分層理論完備形式定理
當已經用到1型變元的量詞(函式量詞)則將增加定義的複雜性,從而引進解析分層。
關於亦有:前束詞中一串同類量詞可收縮成一個;對任一算術謂詞,存在一個原始遞歸謂詞使有扽(,)可表為扽扽((),)即為 扽(,)等事實可以利用。故可將全體解析謂詞依以下形式分類:
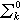 分層理論
分層理論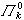 分層理論
分層理論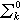 分層理論
分層理論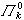 分層理論
分層理論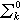 分層理論
分層理論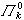 分層理論
分層理論設為一元函式集(嶅),這時我們可以把所考慮的謂詞(,,…,,,,…,)推廣為算術於和解析於中任意有限多個函式的謂詞。這時所得到的相應的分層,分別稱為-算術分層和-解析分層,並且分別記作和
關於集合算術分層和解析分層分別相應於無理數空間中的有限波萊爾集合射影集。J.W.艾迪生稱之為古典描述集合論。與之相應的,關於集合的(即=═時)算術分層和解析分層的理論便稱之為能行描述集合論。
如果只考慮自然數謂詞(即在中,m=0的情形),則可定義()為型謂詞(≥0),它在型的謂詞中具有最高級的遞歸不可解度,且其不可解度確實比()高,因而(=0,1,2,…)決定了遞歸不可解度的算術分層。克林用可構造序數的記法系統把序列推廣到以可構造序數作下標的不可解度分層即遞歸不可解度的超算術分層記作{|∈},如果一函式或謂詞對於某∈,遞歸於,則稱此函式或謂詞是超算術的。使得一謂詞為超算術的其充要條件為它可以在墹姌中表示。
克林套用具有任意型變元(=0,1,2,…)的一般遞歸函式的理論,對具有任意型變元的謂詞建立了分層理論,使得原來的分層理論得到了進一步的推廣。
如果把上述的,,с,…,看成是集合變元(即,,с,…是表示集合的變元)即可得到萊維的分層。
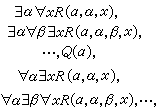 分層理論
分層理論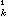 分層理論
分層理論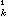 分層理論
分層理論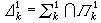 分層理論
分層理論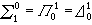 分層理論
分層理論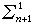 分層理論
分層理論 分層理論
分層理論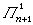 分層理論
分層理論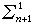 分層理論
分層理論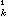 分層理論
分層理論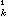 分層理論
分層理論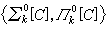 分層理論
分層理論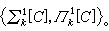 分層理論
分層理論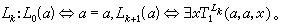 分層理論
分層理論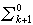 分層理論
分層理論 分層理論
分層理論
