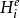分圓類

分圓類(cyclotomic class)是一種等價類，設q為奇素數冪，w為有限域GF(q)的一個原根，若e為q-1的因子，q-1=ef，ε=w^e，則H^e={1，ε，ε²，…，ε^f-1}是GF(q)的乘法子群，將子群H^e的陪集H^e_a=H^ew^a稱為分圓類，這裡a取0，1，…，e-1。

基本介紹

• 中文名：分圓類
• 外文名：cyclotomic class
• 所屬學科：數學（組合學）
• 簡介：一種等價類

基本概念

定義1 設q=ef+1為奇素數冪，F_q為q階有限域，，設w為F_q的本原元，ε=w^e。令

則稱為e次分圓類(cyclotomic classes)。

由定義可知，是的f階乘法子群。而各e次分圓類則是的陪集。以下簡記H^e=。

定義2 設g=ef+1為奇素數冪，對0≤i，j≤e-1，令

稱為e階分圓數(cyclotomic number),當無需指明e時,也常將簡記為。

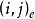
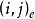
分圓類與差集的構作

引理1(i)；

(ii)

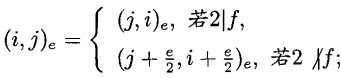
(iii)

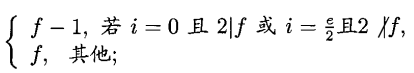
(iv)

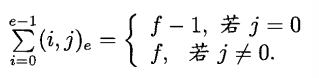
引理2 若且唯若2∈時為奇數。

由引理2可知，在這e個分圓數中，恰有1個為奇數，其餘e-1個均為偶數。

引理3設g∈，則方程

的解的個數恰為(i，0)_e。

定理1(Lehmer)設q=ef+1為奇素數冪，則分圓類H^e為F_q的加法群中差集的充分必要條件是f為奇數且

當上述條件滿足時，H^e是一個-差集。

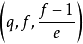
定理2(Lehmer) 設q=ef+1為奇素數冪，則為F_q的加法群中差集的充分必要條件是f為奇數且

當上述條件滿足時，D是一個-差集。