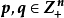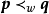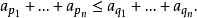基本介紹
- 中文名:凸數列
- 外文名:convex sequence
- 所屬學科:數學
- 簡介:在自然數集上的凸函式
凸數列的定義,相關性質定理,
凸數列的定義
定義1 若實數列{ak}(有限的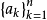 或無限的
或無限的 滿足條件
滿足條件
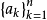

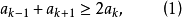
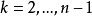
定義2 若非負實數列{ak}(有限的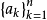 或無限的
或無限的 滿足條件
滿足條件
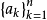

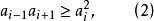
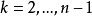
相關性質定理
定理1 若{ak}是一個凸序列,則{Ak}也是一個凸序列,其中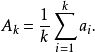
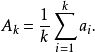
凸數列是凸函式的離散形式,下述三個定理反映了二者的關聯。
定理2 設{ak}是凸數列,f是遞增的凸函式,則{f(ak)}也是凸數。
由題設有
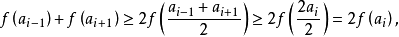
定理3 設φ是R++上的凸函式,則{φ(k)}是凸數列。
如果{ak}是凸序列,則函式φ是[1,∞)上的凸函式,這裡φ的圖象是以(k,ak)(k∈N)為頂點的折線。
定理4 設{ak}是凸數列,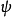 是Ω上的連續的遞增的凸函式。定義函式
是Ω上的連續的遞增的凸函式。定義函式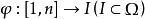 如下妒
如下妒
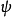
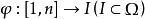
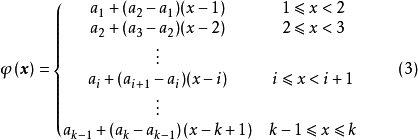
則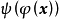 是[1,k]上的連續凸函式,若
是[1,k]上的連續凸函式,若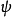 是Ω的連續的遞減的凹函式,則
是Ω的連續的遞減的凹函式,則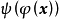 是[1,k]上的連續凹函式。
是[1,k]上的連續凹函式。
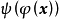
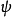
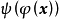
定理5數列{ak}是凸數列的充要條件為:對任意四個非負整數m,n,p,q,當p<m<q,p<n<q,且m+n=p+q時,恆有
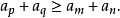
注1 條件p<m<q,p<n<q可放寬為p≤m≤q,p≤n≤q.從控制不等式的觀點來看,條件p≤m≤q,p≤n≤q,且m+n=p+q意味著(m,n)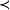 (p,q)。
(p,q)。
很自然想到上述結果是否可推廣到n維情形?石煥南,李大矛建立了如下結果:
定理6 設n≥2,數列{ak}是凸數列的充要條件為: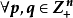 ,若
,若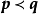 ,恆有
,恆有
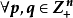
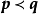
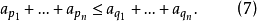
定理7 若數列{ak}是增的凸數列,對於任意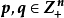 ,若
,若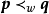 ,則
,則