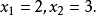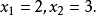冪指方程

諸如x^x=x這樣的方程，既不是整式方程，又不是指數方程，更一般地，如果在方程中出現底數和指數中同有未知數的項，這樣的方程通常叫做冪指方程(power-exponent equation)。冪指方程的求解甚為複雜，通常討論如下兩種簡單情形：限於尋求整數解；底數雖有未知數，但取值恆為正數。

基本介紹

• 中文名：冪指方程
• 外文名：power-exponent equation   
• 所屬學科：數學
• 所屬問題：初等代數
• 特點：底數與指數同時有未知數

基本介紹

冪指方程是一種特殊的指數方程，指在方程中出現乘冪且底數與指數中同時含有未知數的方程，例如x^x=x(x>0)。冪指方程的求解較為複雜，通常只討論如下兩種簡單情形：限於求整數解；作為底數的未知數的函式式恆取正值。例如，解方程

由log₃x知x>0，且方程的右邊在(0，+∞)上有意義，對方程的兩邊取以3為底的對數得

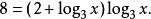
令y=log₃x，得8=(2+y)y。解之有y₁=-4，y₂=2，即log₃x=-4或log₃x=2，所以原方程的解為x₁=1/81，x₂=9。

指導 關於冪指方程的一般解法(分三步) : ①討論確定x的允許取值範圍；②討論底數為0，±1時的情況，適合者為根；③在x的允許取值範圍內，且在x≠0，±1的條件下，按一般指數方程解之。見下文例1。

舉例說明

【例1】解方程:。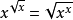

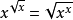
解：第一步:確定x的允許取值範圍。

由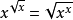知，如有意義，必須x≥0，

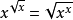
又∵0º無意義，

∴x≠0，因此，x> 0。

第二步:討論底數。

顯然x= 1適合方程。

第三步:在x>0，x≠1的前提下，

由得：

解得:

(不適合，捨去)

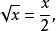
原方程的解為: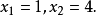

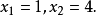
【例2】解方程:。

解 (1) 當x-2<0時，即x<2時，欲使方程兩邊的冪有意義， x-1，3x只能是整數或分母是奇數的既約分數。(負數底數的冪的指數只能取整數或分母是奇數的既約分數)

(2) 當x-2=0，即x= 2時， 適合方程。

∴x=2是原方程的解，

當x-2=1, 即x=3時，適合方程，

當x-2=-1, 即x= 1時，不適合方程。

∴x= 3也是方程的解。

(3)若x為小於2的整數或x>2時，由比較指數法得:3x=x-1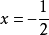，∴，但不是整數也不是分母為奇數的既約分數，不適合方程，應捨去。

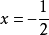
∴原方程的解為: