典型域(classical domain)是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域,它們有四大類和兩個特殊的域,分別在16維及27維復歐氏空間中,這兩個域也稱為例外典型域。
基本介紹
- 中文名:典型域
- 外文名:classical domain
- 所屬學科:數學
- 所屬問題:多複變函數論
- 相關概念:不可分解、全純、有界域等
第一類典型域
第二類典型域
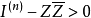
第三類典型域
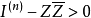
第四類典型域
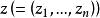
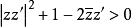
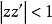
相關介紹

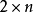
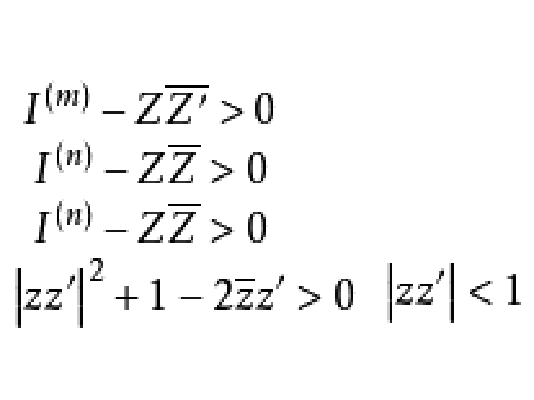
典型域(classical domain)是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域,它們有四大類和兩個特殊的域,分別在16維及27維復歐氏空間中,這兩個域也稱為例外典型域。
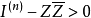
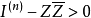
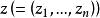
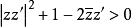
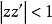

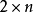
典型域(classical domain)是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域,它們有四大類和兩個特殊的域,分別在16維及27...
第五類例外典型域(exceptional classical do-main of fifth class)是典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的...
華羅庚著,華羅庚以其專著《典型域上的多元複變函數論》獲得1956年度國家自然科學獎一等獎。...
《新農村典型供電模式》是有關供電模式的第一本專著。在界定供電模式含義的基礎上,提出了電網規劃建設基於區域差異化思想發展,確立了新農村供電模式框架。...
第六類例外典型域(exceptional classical do-main of sixth class)是典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的...
域,數學辭彙,定義域,值域,數學名詞,函式經典定義中,因變數改變而改變的取值範圍叫做這個函式的值域,在函式現代定義中是指定義域中所有元素在某個對應法則下對應的...
對稱有界域是研究得最深入的一類齊性有界域。Cn中的域稱為對稱有界域,如果它關於伯格曼度量為對稱埃爾米特流形。對稱有界域為齊性有界域,它雙全純同構於不可...
陸啟鏗還出版過《多複變函數引理》,《典型流形與典型域》、《微分幾何學及其在物理學中的套用》。陸啟鏗作為華羅庚先生歸國後的第一批親傳弟子,憑藉自己的執著和...
華羅庚一生留下了十部巨著:《堆壘素數論》、《指數和的估價及其在數論中的套用》、《多複變函數論中的典型域的調和分析》、《數論導引》、《典型群》(與萬哲先...
求實務本是其典型的外在特徵;窄長院落、單坡屋頂、厚重牆體構成其獨有地域技術範式;氣候水土、自然屬性、文化觀念與厚重歷史都成為關中民居外在特徵形成的內在基因...
企業物流是指企業內部的物品實體流動。它從企業角度上研究與之有關的物流活動,是具體的、微觀的物流活動的典型領域。企業物流又可區分以下不同典型的具體物流活動:...
亞洲的溫帶大 溫帶大陸性氣候生物情況 陸性氣候特徵最為典型。首先,亞洲的廣大內陸地區和高緯地區與其它大陸同緯地區相比,具有冬寒夏熱、春秋短促、氣溫年較差極大、...
但長山山脈東西兩部有明顯不同 : 西部降水季節分配近似印度半島,乾濕兩季較明顯,而東部降水季節分配同菲律賓群島相似,乾濕兩季不典型。東部內陸地區自然植被以熱帶季...
中國生態功能區劃資料庫和典型區域綜合生態資料庫,是集基礎數據資源集成、研究成果展示為一體,構建二維和三維WebGIS 系統,提供空間數據和研究成果查詢與三維可視化展示...
分析了目前東北地區經濟發展現狀與問題;結合歐、美、日等已開發國家典型老工業基地開發、衰退與改造的經驗,研究了東北地區經濟發展傳統經濟成長模式的不可持續性與經濟...
5.1典型區域的選擇 5.2江兩省綜合減災能力評價示範 5.3雲南省綜合減災能力評價示範 5.4區域綜合減災能力評價模型的驗證 第6章基於減災能力評價的洪澇災害綜...
