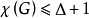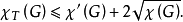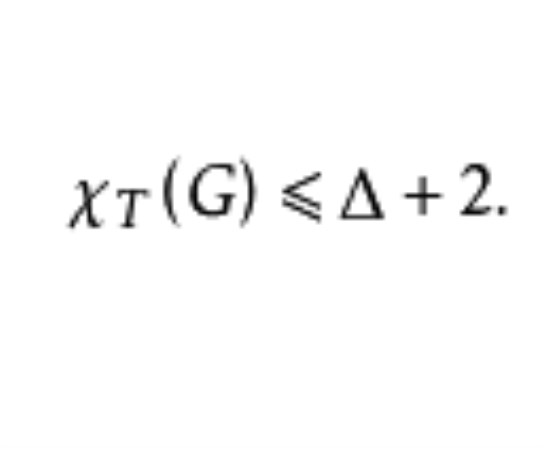全著色猜想

色數指圖的所有同類型的正常著色，用的顏色的數目最少的那種正常著色所用顏色數目，一個圖G的點正常著色的色數稱為點色數或簡稱色數，常用χ(G)表示圖G的色數，圖G的邊色數是指G的邊正常著色的色數，G的邊色數常記為χ′(G)，平面圖G的面色數就是G的面正常著色的色數，常記為χ*(G)，圖G的全色數就是G的正常全著色的色數，常記為χ_T(G)，全著色猜想就是：對任意簡單圖G，χ_T(G)≤Δ(G)+2，Δ(G)表示G中節點的最大次，已經證明：對於任何n階圖G，當Δ(G)≤4或Δ(G)≥n-5時，全著色猜想成立，圖G的n色數指如下著色的最少色數：用若干種色，對圖G的節點著色，使得G上每條長度為n的路上沒有兩個節點著同一色.G的n色數常記為χⁿ(G)，類似地，定義n邊色數和n全色數，一個圖G完全著色是指G的這樣一種點正常著色，使得對於這一種著色的任何兩色，都存在G的一邊，它的兩個端點恰著此兩色，圖G的完全著色數，就是指在G的所有完全著色中，所用顏色數目最少的那一種完全著色的顏色數，若圖G本身不是完全圖，則將它的不相鄰的兩節點等同為一個節點；若所得到的圖仍不是完全圖，則繼續做這種運算，直到所得的圖為完全圖，一個圖，通過這種運算將它變為完全圖所需要的最小運算次數稱為G的消色數，換言之，G的消色數就是將G變換到完全圖所需要做的初等同態的最小次數。

基本介紹

• 中文名：全著色猜想
• 外文名：total coloring conjecture
• 所屬學科：數學
• 所屬問題：組合學(圖與超圖)

基本介紹

設為一個簡單圖，一個函式被稱為圖G的一個正常k-全著色函式，如果滿足以下條件：

(1)對任意相鄰的兩個點，均有；

(2)對任意相鄰的兩條邊2，均有；

(3)對任意一條邊'及其關聯的點u和v，均有且。

圖G的全色數定義為：{k|存在圖G的正常k-全著色函式}。

由圖的全著色定義，不難看出下面的性質：

(1)對任何簡單圖，其中T(G)表示G的全圖；

(2)對任何簡單圖；

(3)對任何簡單圖，其中表示G的最大度。一般來說，確定一個圖的全色數是非常困難的，目前只有一些特殊圖的全色數被確定，如完全圖、樹和圈等。大多數工作都是研究全色數的上界。在1965年Behzad在他的博士論文中提出了如下一個猜想，後來被人們稱為全著色猜想，至今未能解決。

全著色猜想 對於任何簡單圖G，均有

Δ表示G中節點的最大次。

相關性質定理

圍繞這一著名猜想，人們對全著色問題進行了深入的研究：一方面，研究全著色猜想對一些特殊圖類的正確性；另一方面，給出一般圖的全色數的上界，並不斷改進。張忠輔等人研究全著色時，按全色數定義了兩類圖。即第一類圖集和第二類圖集。即

可見，全著色猜想等價於：對於任何簡單圖G，均有。

眾所周知，對任何簡單圖G，均有，且。由性質(2)可得，這是一個平凡的上界，人們關心的是對此上界能有多大的改進。

定理1 設G為簡單圖G，且，則有

定理2 設G為n階簡單圖，則

定理3 設G為n階簡單圖，則

定理4 對任意p階簡單圖G，均有

對於任何非空的簡單偶圖G,由於且，故由性質(2)知

即全著色猜想對偶圖成立。