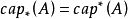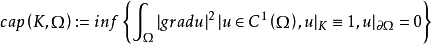內容量

內容量是集合的一種度量。

基本介紹

• 中文名：內容量
• 外文名：inner capacity
• 適用範圍：數理科學

定義

的任意子集 A 的內容量 (inner capacity) 是cap_*(A)=sup{cap(B)|BA，B是緊急}。

容量

[capacity]

簡介

對於 中有界開集Ω 的緊子集 K，令

設 B(0,R) 是原點為中心 R 為半徑的球。當 時，極限存在，定義為緊急 K 的容量cap(K)。

性質

緊急 K 的容量 cap(K) 有以下基本性質：

(1) 當 ，有 ；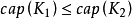

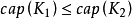
(2)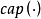 是有強次可加的，即對於任意的緊集 A 和 B，有

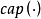
(3) 右連續，對於任意的ε > 0，存在開集ω 使得緊集 K‘ 滿足 ，有 。

定義在可分拓撲空間上的緊子集累上的函式如果滿足以上三條，則被稱作肖凱（Choquet）容量。

的任意子集 A 的內容量 (inner capacity) 是cap_*(A)=sup{cap(B)|B A，B是緊急}。

的任意子集 A 的外容量 (outer capacity)是cap*(A)=sup{cap*(B)|B A，B是開急}，

這裡對於開集 B，cap*(B) 定義為 sup{cap(E)|E B，E 是緊急}。

的子集 A 稱作 可賦容量的 ( capacitable ) 如果它的內容量等於外容量： 。這個數稱作 A 的容量，記為 cap(A)。

中所有博雷爾和解析集都是可賦容量的。cap(A) 在平移和旋轉變換下不變，但不是可加的。