基本介紹
- 中文名:克羅內克指數
- 外文名:Kronecker index
- 領域:數學
- 學科:抽象幾何
- 性質:指標
- 條件:流形
概念,流形,上同調類,人物簡介———克羅內克,
概念
克羅內克指數(Kronecker index)是一種特定的指標。設M是閉連通光滑n維流形。利用模2係數,存在一個基本同調類μM∈Hn(M,Z/2),故對任意上同調類V∈H(M,Z/2),定義克羅內克指數為:

流形
流形是一類特殊的連通、豪斯多夫仿緊的拓撲空間,在此空間每一點的鄰近預先建立了坐標系,使得任何兩個(局部)坐標系間的坐標變換都是連續的。n維流形的概念在18世紀法國數學家拉格朗日的力學研究中已有萌芽。19世紀中葉英國數學家凱萊(1843)、德國數學家格拉斯曼(1844,1861)、瑞士數學家施勒夫利(1852)分別論述了n維歐幾里得空間理論,把它視為n個實變數的連續統。1854年德國數學家黎曼在研究微分幾何時用歸納構造法給出一般n維流形的概念:n維流形是把無限多個(n-1)維流形按照一維流形方式放在一起而形成的,從此開始流形的拓撲結構及其局部理論的研究。法國數學家龐加萊在19世紀末把n維流形定義為一種連通的拓撲空間,其中每一點都具有和n維歐氏空間同胚的鄰域(被稱為龐加萊流形),從而開闢了組合拓撲學的道路。
對流形的深入研究集中在流形上的微分結構與組合結構的存在性、唯一性問題,微分結構與組合結構的關係,流形的各種意義下的分類等問題,20世紀50—60年代做出許多重要結果,近幾十年來出現有限維帶邊流形和無限維流形概念。流形理論在與其他拓撲理論的相互結合發展中也提出許多問題,其研究仍在繼續。
流形也是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可微流形的研究,在點集拓撲中已經熟悉把一元或多元連續函式的概念,推廣為拓撲空間之間連續映射的概念。但是對於函式的可微性,在進行類似的推廣時,卻遇到截然不同的情況,若M,N為拓撲空間,f:M→N為映射,則為了計算微商,須考慮(f(x+h)-f(x))/h,然而在一般空間中,這是沒有意義的,因此對於M與N,提出了有一個支撐空間的要求,這是產生可微流形概念的客觀要求。
上同調類
上同調類的概念可以由上同調模的概念得出。上同調模是一種重要的模。指由上復形給出的模。設:
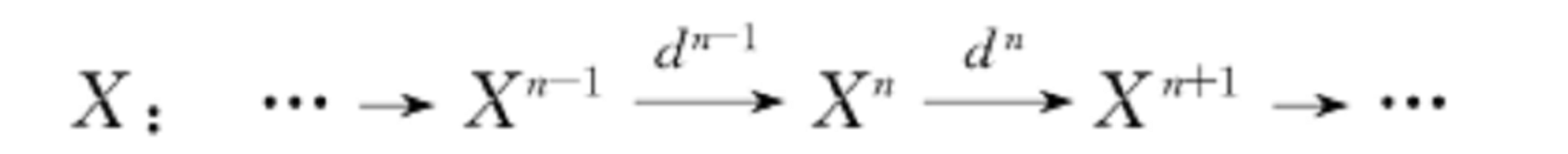
是環A上的復形,因為dd=0,所以Im dker d,於是H(X)=ker d/Im d為A模,稱此模為上復形X的上同調模。分別以Z(X),B(X)來表示ker d,Im d,把X,Z,B,H的元素分別稱為上鏈、上循環、上邊緣、上同調類。若X是環A上的復形,則對偶地可以定義復形X的同調模Hn(X)=ker dn/Im dn+1,把Xn,Zn,Bn,Hn的元素分別稱為鏈、循環、邊緣、同調類。
人物簡介———克羅內克
克羅內克是一位德國數學家。生於利格尼茨,卒於柏林。1841年入柏林大學,選學數學、天文、化學和哲學等課程,曾參加學生的民主活動。1845年以關於代數數域的研究論文獲博士學位。之後返鄉繼承遺產,經營田莊和銀行,其間仍以研究數學自娛。1855年重返柏林,以很快的速度發表一系列論文,內容涉及數論、橢圓函式論和代數學,特別探討了這些學科的相互依賴性。1861年被選為柏林科學院院士。1883年受聘為柏林大學教授。1884年當選為英國皇家學會會員。他還是法國科學院和聖彼得堡科學院外籍院士。克羅內克的主要貢獻在數論、代數學、函式論、拓撲學等方面;努力統一數論、代數學和分析學的研究;深入探討橢圓模函式理論,並用它解出了一般的五次方程;發展了庫默爾的“理想數”理論,創立了有理函式域論,引進了在域上添加代數量生成擴域的概念和模系的概念,因而使代數數的理論獨立於代數基本定理;發現有理數域的任一阿貝爾擴張一定是一分圓域的子域,並提出著名猜想(見克羅內克青春之夢):橢圓函式具有複數乘法的模方程與虛二次域的阿貝爾擴張有類似性。他還提出研究代數曲線的重要方法。在數學基礎的大論戰中,他是直覺主義數學流派的代表人物之一,曾激烈反對過外爾斯特拉斯和G.康托爾等人的觀點,主張數學的算術化。他的數學觀對後世有極大影響。他的一句名言是:“上帝創造了整數,其他一切都是人為的。”反映了他對當時的分析學持批判態度。他的著作由亨澤爾編輯,以《克羅內克全集》(5卷,1895—1931)出版。

