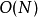基本介紹
- 中文名：元胞列表
- 外文名：Cell lists
- 學科：電子工程
算法,周期性邊界條件,幽靈元胞,校正向量,改進,
算法
元胞列表的思想是將體系分解為更小的元胞單元，只需計算計算相同和相鄰元胞中的粒子距離而不再需要對整個體系中所有其他粒子求解，元胞的邊長不小於粒子截斷半徑{\displaystyle R_{c}}，以此保證所有相互作用著的粒子作用力計算沒有遺漏。
根據元胞列表計算近鄰粒子間非鍵相互作用的基本算法如下：
for all近鄰元胞對
do
for all
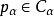do
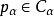
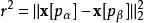
if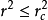
then
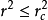
end if
計算
與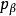
間相互作用。
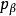
for all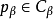
do
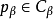
end for
end for
end for
元胞的個數取決於模擬體系的尺度和粒子截斷半徑，每個元胞內粒子數
，與體系大小近似無關，兩個元胞間粒子作用計算的複雜度為
，整體複雜度為
，與未運用元胞列表時的
相比有了顯著的降低。
以Fortran描述的構建列表的算法如下：
subroutine new_nlist rn = box/int(box/rc) ! 計算一個方向上的元胞個數。box為體系長度，rc為截斷半徑 do icel=0 , ncel - 1 hoc(icel) = 0 ! 對每一個元胞的鏈頭置0 end do do i = 1 , npart ! 掃描所有粒子 icel = int(x(i)/rn) ! 確定粒子所在的元胞編號 ll(i) = hoc（icel）! 連結icel元胞的鏈頭 hoc(icel) = i ! 將粒子編號i添加到鏈頭 end doend subroutine
周期性邊界條件
在多數情況下，模擬的體系都會引入周期性邊界條件以避免不合實際的邊界。在樸素的算法中，對於每次粒子間距離計算都要運用此條件：
dx = dx - Lx*ANINT(dx/Lx)dy = dy - Ly*ANINT(dy/Ly)dz = dz - Lz*ANINT(dz/Lz)
造成很大的時間開銷。元胞列表的引入可改進這一問題，主要有“幽靈元胞”和校正向量兩種最佳化方案。
幽靈元胞
幽靈元胞通過在邊界以外複製一層元胞解決周期性邊界條件問題，這些複製的元胞擁有與原元胞完全相同的信息，這樣在計算距離時就不再需要考慮周期性邊界條件。此做法導致邊界上的粒子的計算量會增加一倍（元胞在三維盒子的面上）甚至更多（元胞在三維盒子的棱或頂角），但這種方法非常直觀且易於並行。
校正向量
由於元胞的邊界條件和粒子距離的邊界條件是一致的，因此在搜尋近鄰元胞對時可導出一個向量
來校正粒子間距離的計算。對於屬於兩個近鄰元胞的兩個粒子
與
，它們之間的距離按此式得出：
校正向量可以在掃描元胞時計算，也可在初始化時儲存。此方法單核效率通常高於幽靈元胞，但其實現相對複雜，並且將計算距離的開銷部分轉移到掃描元胞中。
改進
在最初的元胞列表中，每一個粒子會與27個元胞作用，體積為
，相較截斷半徑球
，有84%的距離計算是不必要的。雖然複雜度從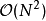
降至
，但複雜度的係數項不容忽略。一種簡單的改進方法是減小元胞長度，取元胞大小為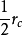
，掃描時計算近鄰和次近鄰兩層元胞共
個元胞，則距離計算包含的體積降為
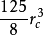，距離計算的體積下降了將近一倍。然而，元胞的掃描具有
的複雜度，元胞劃分數進一步增大帶來的性能提升很快被掃描元胞的開銷浪費掉。
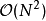
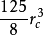
將韋爾萊表與元胞列表聯合，達到進一步的改進。使用元胞列表構建韋爾萊表可使後者更新的複雜度降為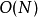
，同時克服了掃描元胞的時間開銷。
