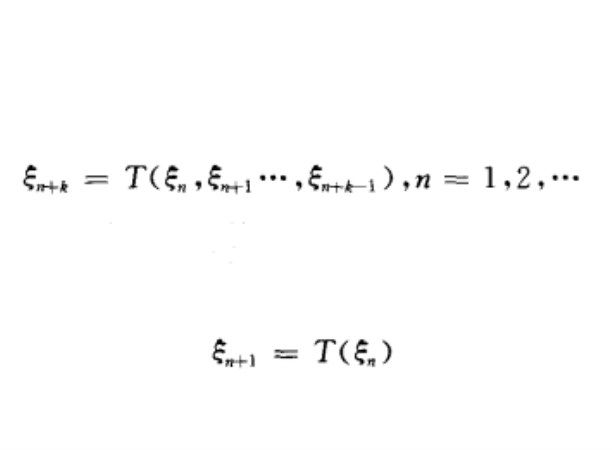偽隨機數周期是指具有周期性循環往復的偽隨機數列中不重複偽隨機數的個數，或產生偽隨機數疊代過程中一個循環所含數字個數。用某遞推公式按一定程式產生偽隨機數，一般從某—初始值起步產生偽隨機數列x1，x2，…；若存在m，使對任意n，有xn+m=xn(n=1，2…)，則滿足上述關係的最小m稱做偽隨機數的周期。選擇產生偽隨機數的遞推公式時，要求周期充分長。
基本介紹
- 中文名：偽隨機數周期
- 外文名：pseudo random numbersperiod
- 所屬學科：數理科學
- 概念：周期性循環現象的偽隨機數個數
基本介紹,偽隨機數的周期和最大容量,
基本介紹
發生周期性循環現象的偽隨機數個數，稱為偽隨機數的周期。
偽隨機數亦稱擬隨機數、準隨機數。按照不同於隨機性原則的一定規則或程式，用數學方法通過選定的遞推關係和疊代過程產生的，具有與隨機數相似性質的數字。產生偽隨機數的常用數學方法，有同餘法、移位法、取中法、無理數的十進分解法....等。在數字計算機上用數學方法產生偽隨機數，每到產生一定數量的偽隨機數之後，出現循環重複的周期現象或退化為0的退化現象。對這類數學方法的一般要求為，1.產生偽隨機數的周期一不重複偽隨機數的數量一一應充分地長；2.產生隨機數的速度要快，而所占用的記憶體要少；3.所產生的偽隨機數具有所需要的統計性質——隨機性和與給定分布律的一致性。嚴格地說，用任何數學方法疊代產生的偽隨機數，都不是真正的隨機數。不過在許多實際套用中，假如偽隨機數的周期充分長，且通過相應的統計檢驗在一定顯著性水平下可以認為，所得偽隨機數滿足隨機性假設和與給定分布的--致性(擬合)假設，則這樣的偽隨機數可以代替隨機數使用。
偽隨機數的周期和最大容量
用來產生隨機數的方法的數學方法，亦即用遞推公式：
，對於給定的初始值
，確定
，經常遇到的是k=1情況，這時的遞推公式是
，對於給定的初始值
，確定
。
用數學方法產生的隨機數存在兩個問題
(i)遞推公式和初始值
確定後，整個隨機數序列便被唯一確定下來了。或者說，隨機數序列中除前k個隨機數是選定的外，任意一個隨機數
，被前面的隨機數唯一確定了,不滿足隨機數相互獨立的要求。
(ii)的既然隨機數序列是用遞推公式確定的，而在電子計算機上所能表示的[0，1]上的數又是有限多的，因此，這樣的隨機數序列就不可能不出現重複地無限繼續下去，一旦出現了這樣的n'和n''，n'<n''，使得如下等式成立
由於這兩個原因，常稱用數學方法所產生的隨機數為偽隨機數。
關於偽隨機數的第一個問題，不能從本質上加以改變；但是，只要產生偽隨機數的遞推公式選得比較好，隨機數的相互獨立性是可以近似地滿足的。至於第二個問題，則不是本質上的，因為用蒙特卡羅方法解決任何問題時，所用隨機數的個數總是有限多個的，只要其個數不超過偽隨機數序列出現循環現象時的長度就可以了。用數學方法產生偽隨機數非常容易在電子計算機上實現，可以復算，而且不受電子計算機限制，因此，雖然存在著一些問題，但是仍然被廣泛地在電子計算機上使用，是在電子計算機上產生隨機數的最主要方法。
偽隨機數的周期和最大容量
由於偽隨機數序列一定會出現周期性的循環現象，因此，在使用偽隨機數的時候不可能無限制地繼續下去，就是說由偽隨機數所組成的子樣容量應有一個最大限度，超過這個限度將出現偽隨機數的重複。發生周期性循環現象的偽隨機數個數，稱為偽隨機。數的周期，根據(1)式，偽隨機數的周期等於n''-n'，從偽隨機數序列的初始值開始，到出現循環現象時為止，所產生的偽隨機數的個數n''稱為偽隨機數的最大容量。
