偶奇比猜想

偶奇比猜想是指所有偶數之積與所有奇數之積的比值。

基本介紹

• 中文名：偶奇比猜想

猜想介紹

我們知道所有偶數之積與所有奇數之積的比值是個發散的，但是如果我們把這個值除以最大偶數除以2後的方根時情況就發生了變化。它會趨於一個常數。那么是否存在一個極限υ，使得下面級數存在一個極限呢？通過大量計算我們得到精度很高的逼近函式公式如下：

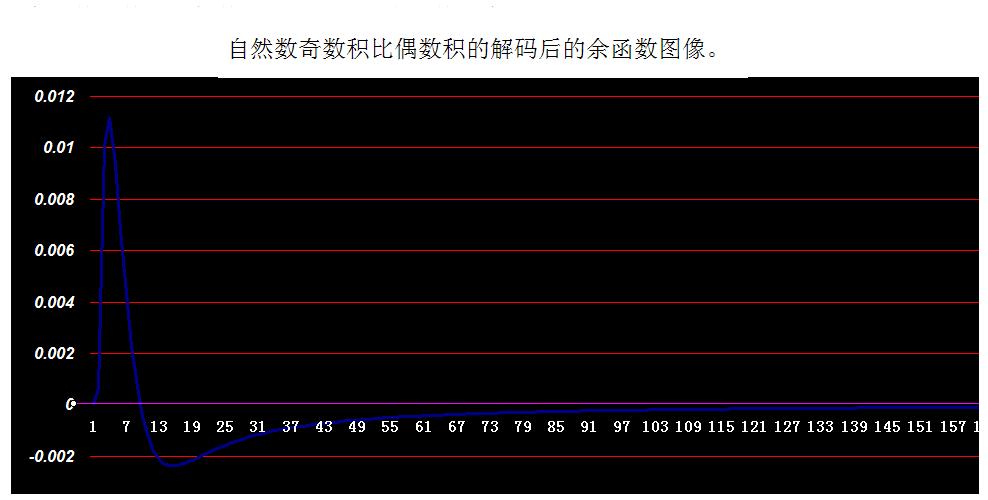
ε(n) 是解碼後的余函式，詳詞條圖片

函式極限

對以上函式求極限我們得到

套用

由三角函式積分我們得到以下恆等式

那么以上積分我們得到它的近似值公式如下

誤差說明

原解碼函式n=1時誤差為0，n=2時誤差為-0.00493898954609273，也是函式的最大誤差n∈(3,40)誤差在 0.00303628416768742到7.60400410371176E-06之間，其中n=3 時誤差最大為0.00303628416768742

n>=41時誤差為負數，就是說解碼函式便大於原函式，但誤差均小於-0.000220235015010672，最大誤差對 應點是n=171,其他誤差均小於此數，

n在983039附近,-5.99267673351278E-06。。。解碼逼近函式誤差滿足一般工程的要求。。。。

拓展套用

由以上公式我們可以推導出以下恆等式：

譬如

由此計算出，0.5!=0.886274951380842=,誤差為0.0000480259280840611

通過計算，也驗證了逼近公式的準確性，誤差的參數是兩個參數插值造成的偏差。不過一般階乘數值小時不用如此計算，但是大數階乘此公式還是可以利用的。

偶奇比與階乘之間的恆等式

聯立偶奇比與階乘的逼近函式，我們得到以下恆等式

是函式在x點處的余函式值，也是誤差值

指數與階乘的關係式如下：

其餘函式圖象詳自然數密碼詞條

自然數奇偶比逼近公式

余函式圖像如下圖：

通過以上兩個逼近公式，我們得到一個恆等式：

合數質因子分布區間公式

括弧內兩個數與共同構成2n+1的可能質因子的區間點，多數在這幾個數附近。。此公式是以上兩個公式乘積得來的，如果是質數，在這幾個區間均無質因子。。。。奇數最大可能的質因子是n/3,最小質因子在以上兩數最小的一個附近。。。