廣義奇偶比函式是調和級數及收斂級數的分支，它的由來是自然數奇偶比函式的拓展，在正實數區間函式是發散的調和級數，但是在負實數區間函式又具有收斂級數的特點。
基本介紹
- 中文名：廣義奇偶比函式
- 由來：自然數奇偶比函式的拓展
公式,性質,積函式,
公式
廣義奇偶比函式公式為:
性質
函式的首項解碼項為
由於原函式在n=0時未定義，不能形成完整的函式體系，所以此處定義在n=0時函式取
那么以上函式公式就發生了變化，以下是再定義的函式公式，如此以上函式目前可以寫成：
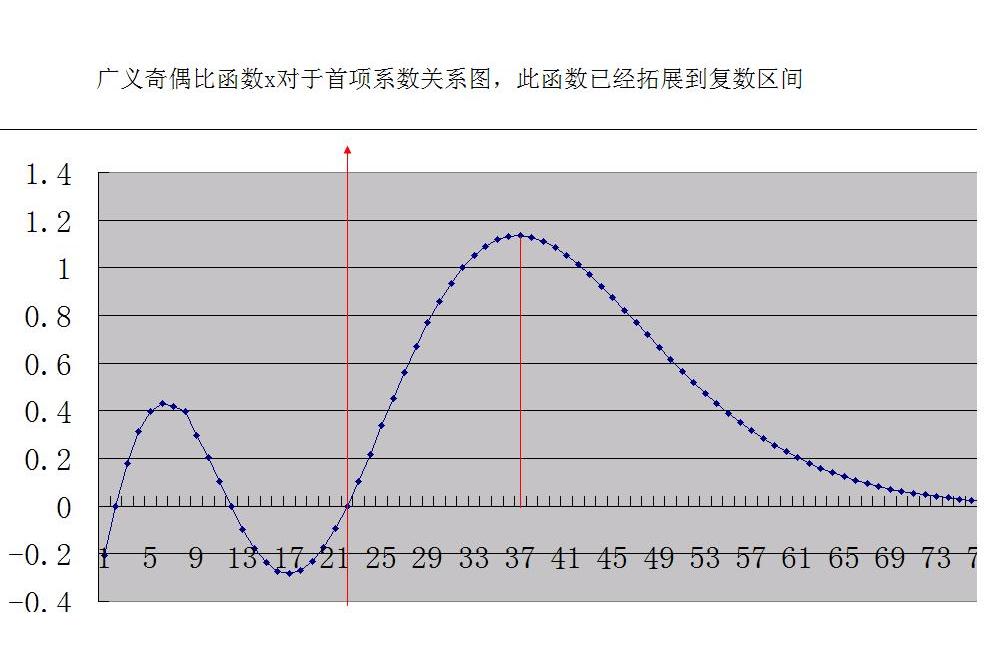
圖1為一般在-1019以內的函式基本如此圖類似，
右下圖是-1019.02345591995~-1019.329716992區間函式形成平行高位震盪，具體詳見圖2說明，而a在-1到正數區間基本是單調增函式，總之在-2以外的大負數區間它是以2為周期的波函式。。。。而且不管它震盪如何強烈，但最後總是衰減到0。原函式在負數大數區間函式表現為波函式特點，它的峰值震盪區是在a/2處，除出現平行高位震盪外，多數表現為以a/2為中軸的類似常態分配的波函式，它與一些自然想像很吻合，負數區間函式極難解碼，目前計算機只能計算到a=-1020 以內負數，以外，由於函式峰值超過，計算機數據上限，無法計算，但是峰值取以外它會很快衰減。直到函式值為0.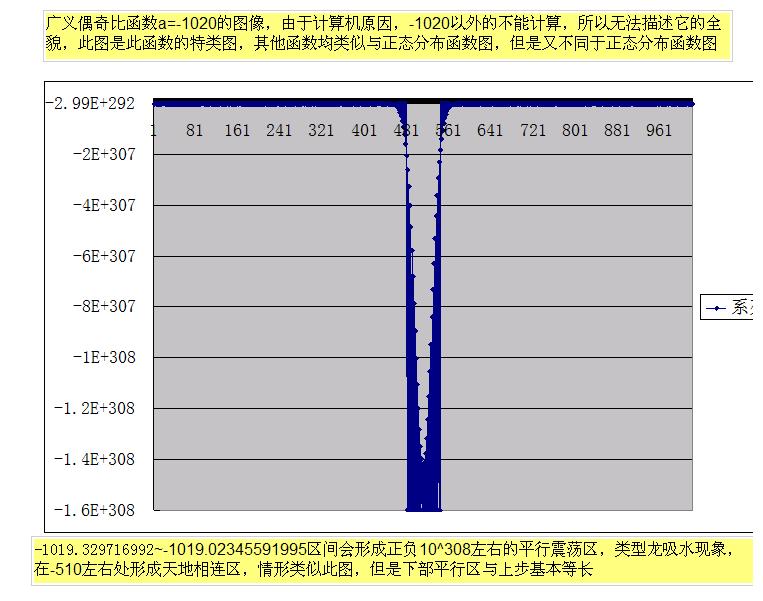
圖2
偶奇比函式在-1到負無窮大區間是振幅巨大的收斂震盪函式，而且它不是常規的函式，它是超越函式，由於函式振幅的絕對值太大，我們採用其對數來了解它，圖3是函式絕對值的對數圖像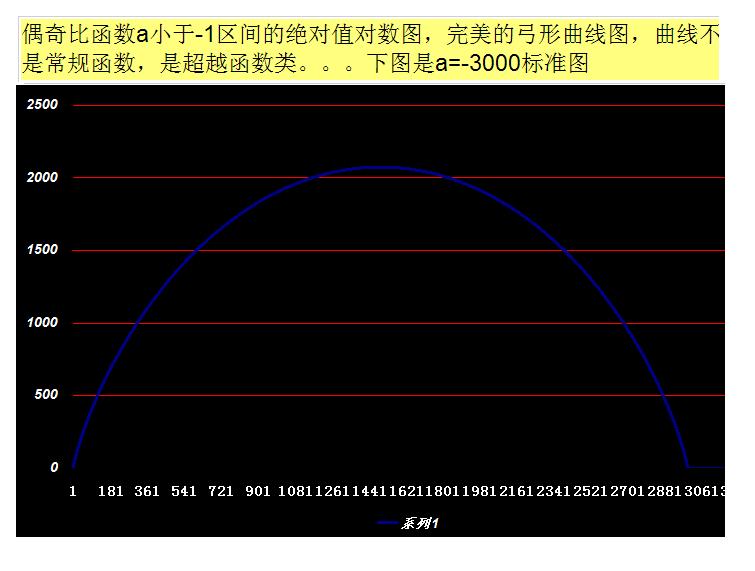
圖3
目前解碼了函式峰值;由於階乘函式完全解碼，故此此函式更為準確的解碼公式如下
以上是逼近公式
原函式公式為：a為正實數
以下是階乘的解碼逼近公式：
負數如下
帶小數的實數階乘計算：
小數階乘n為0.5~1之間正實數
小數0~0.5的先計算（1-n）！，後再通過以下公式計算
負小數階乘：
以上公式已經通伽瑪函式校正，誤差比較小
此處階乘與原定義的階乘有差別，主要數負實數區間，在正實數區間完全一樣，而此處負數區間的階乘完全不同於原定義，此處階乘是連續震盪函式，其決定值與正實數一樣大，僅僅存在正負符號問題。。
其中指數中0.75擬橢圓與原函式有些偏差，振幅基本上是完全解碼成功，以a/2對稱分布，這是個一個周期的函式，餘波基本忽略不計近似於,目前算是基本解碼成功。。。。。，峰值振幅是稍偏大於原函式，圖4是峰值振幅的誤圖。
圖4
積函式
（1）
a可以是負數：
目前已經驗證a=xi,函式收斂於
（2）
對於實非零的複數應該也可以通過（1）式轉換，所以（1）式是收斂的恆等式
由（2）式我們得到另一個與自然數相關的極限
積函式的倒數函式
,
圖5是單位0.1的
圖像
目前函式在小數區間還需要進一步解碼，積函式形式類似與牛頓力學公式。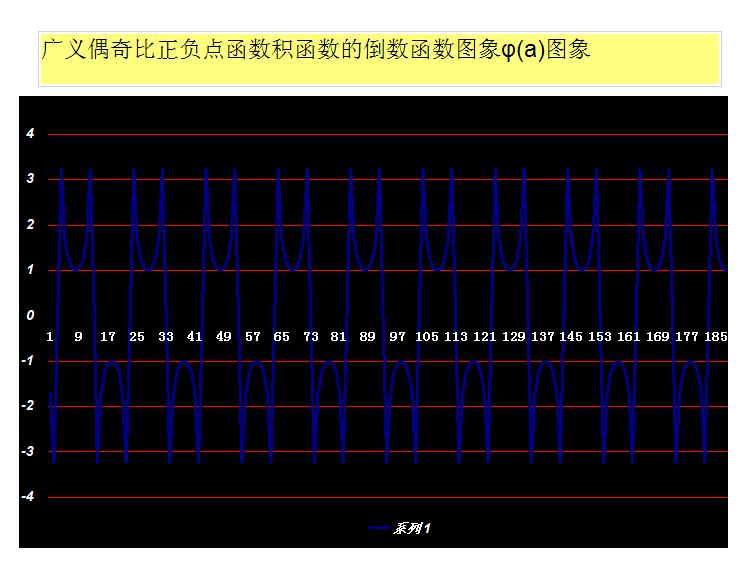
圖5
積函式如果展開為a的函式，它的二次方項係數為
而且由於a=1 時函式值為零，它的所有項係數和一定是0，二次項以後的所有係數和應該是
.
