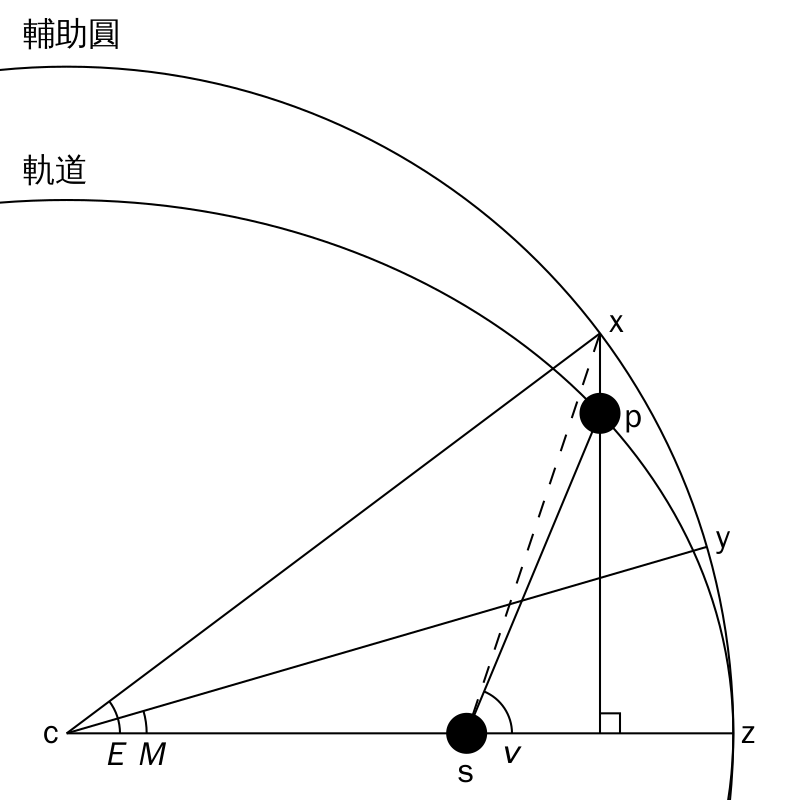
偏近點角是在軌道上的天體所在的位置投影在垂直於橢圓半長軸的外接圓上,並從橢圓的中心量度和近拱點(periapsis)方向之間的角度。在下圖中的標示為E(角zcx)。
基本介紹
- 中文名:偏近點角
- 外文名:Eccentric Anomaly/Elliptic Anomaly
- 別稱:橢圓偏角
計算,簡介,
計算
在太空動力學,偏近點角E可以由下式計算得到:
- {\displaystyle E=\arccos {{1-\left|\mathbf {r} \right|/a} \over e}}
此處:
- {\displaystyle \mathbf {r} \,\!}是軌道上天體的位置向量。(線段sp),
- {\displaystyle a\,\!}是軌道的半長軸(線段cz),和
- {\displaystyle e\,\!}是軌道的離心率。
對平近點角M,E和M的關係是:
- {\displaystyle M=E-e\cdot \sin {E}.\,\!}
這個方程式可以重新解出,從{\displaystyle E_{0}=M}開始,並使用{\displaystyle E_{i+1}=M+e\,\sin E_{i}}的關係。
將這個方程式的{\displaystyle e}以級數展開,當{\displaystyle e<0.6627434}時,最初的幾項是:
- {\displaystyle E_{1}=M+e\,\sin M}
- {\displaystyle E_{2}=M+e\,\sin M+{\frac {1}{2}}e^{2}\sin 2M}
- {\displaystyle E_{3}=M+e\,\sin M+{\frac {1}{2}}e^{2}\sin 2M+{\frac {1}{8}}e^{3}(3\sin 3M-\sin M)}.
還有其他更有效率的解決方法,可以作為推導的參考(參見Murray and Dermott ,1999, p.35),詳細的推導過程和{\displaystyle e}在數學上的極限值可以參考Plummer (1960, section 46)。
對真近點角T,E和T的關係是:
- {\displaystyle \cos {T}={{\cos {E}-e} \over {1-e\cdot \cos {E}}}}
或相等於
- {\displaystyle \tan {T \over 2}={\sqrt {{1+e} \over {1-e}}}\tan {E \over 2}.\,}
半徑(位置向量大小)和近點角的關係是:
- {\displaystyle r=a\left(1-e\cdot \cos {E}\right)\,\!}
和
- {\displaystyle r=a{(1-e^{2}) \over (1+e\cdot \cos {T})}.\,\!}
簡介
偏近點角是過橢圓上的任意一點,垂直於橢圓半長軸,交半長軸外接圓的點到原點的直線與半長軸所成夾角。
在橢圓的參數方程x=acosθ , y=bsinθ中,參數角θ即為偏近點角。
在天體力學中,偏近點角可用來描述極徑。