信道編碼方法是對信源或信源編碼器的輸出進行變換,以期達到或逼近信道編碼定理理論結果的方法。仙農的廣義編碼中包括糾錯編、解碼和調製、解調部分,但通常的信道編碼僅指用於提高通信可靠性,即能檢出和(或)糾正傳輸中出現錯誤的編碼。
基本介紹
- 中文名:信道編碼方法
- 外文名:channel coding method
- 套用學科:通信
目的
分類
分組碼
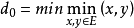
信道編碼方法是對信源或信源編碼器的輸出進行變換,以期達到或逼近信道編碼定理理論結果的方法。仙農的廣義編碼中包括糾錯編、解碼和調製、解調部分,但通常的信道編碼僅指用於提高通信可靠性,即能檢出和(或)糾正傳輸中出現錯誤的編碼。
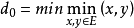
通過信道編碼器和解碼器實現的用於提高信道可靠性的理論和方法。資訊理論的內容之一。信道編碼大致分為兩類 :①信道編碼定理,從理論上解決理想編碼器、解碼器的存在...
信道編碼方法是對信源或信源編碼器的輸出進行變換,以期達到或逼近信道編碼定理理論結果的方法。仙農的廣義編碼中包括糾錯編、解碼和調製、解調部分,但通常的信道...
信道編碼技術是指包括前向糾錯、交織編碼等的技術,它可使移動通信系統工作在低載乾比和高噪聲環境。利用數位訊號處理技術可以很方便地實現信道自適應均衡、分集和...
信道碼是提高信息傳輸時的抗干擾能力以增加信息傳輸的可靠性的一種編碼。在通信工程中,信道碼也被稱為數據傳輸碼或差錯控制碼。...
一般資訊理論的書上都會有信源編碼和信道編碼的具體講解,包括具體的編碼方法。信源編碼專業表述 編輯 既然信源編碼的基本目的是提高碼字序列中碼元的平均信息量,那么,...
信道編碼是通過在被傳輸的數據中引入冗餘位,來避免數位訊號在傳送過程中出現誤碼。用於檢測錯誤的信道編碼被稱為檢錯編碼,而既可檢錯又可糾錯的信道編碼被稱作糾錯...
編碼理論是數學和計算機科學的一個分支,處理在噪聲信道傳送資料時的錯誤傾向。按照編碼理論,資料傳送時會採用更好的方法以修正傳送途中所產生的大量錯誤。編碼共分兩...
差錯控制編碼是指在實際信道上傳輸數位訊號時,由於信道傳輸特性不理想及加性噪聲的影響,所收到的數位訊號不可避免地會發生錯誤。為了在已知信噪比的情況下達到一定的...
圖2 交織編碼示例 GSM中使用這種比特交織器。其交織方式為將信道編碼後的每20ms的數據塊m=456b拆分到8組中,每組57b,然後這每組57 b分配到不同的Burst中。3、...
理論,共11章,內容包括:信息的基本概念、信源及其信息量、信道及其容量、信息率失真函式、信源編碼和信道編碼定理、網路資訊理論以及信源編碼和信道編碼的理論與方法。...
針對不同的傳輸信道或控制信息,LTE系統支持不同的信道編碼方式,如咬尾(Tailbiting)卷積碼、Turbo碼、塊編碼和重複編碼。其中上行/下行共享信道(UL-SCH/DL-SCH)、...
在信道編碼研究的初期,人們探索、研究出各種各樣的編碼構造方法,其中包括卷積碼。早在1955年,P.Elias首先提出了卷積碼。但是它又經歷了十幾年的研究以後,才開始...
在遠程通信、資訊理論、編碼理論中,前向糾錯碼(FEC)和信道編碼是在不可靠或強噪聲干擾的信道中傳輸數據時用來控制錯誤的一項技術,前向糾錯編碼技術(FEC)具有引入級聯...
同時香農三大定律是資訊理論的基礎,雖然沒有提出具體的編碼實現方法,但是為通信信息的研究指明了方向。他的“信道容量定理”指出,可以找到這樣一種技術,當數據傳輸速率...
香農三大定理是資訊理論的基礎理論。香農三大定理是存在性定理,雖然並沒有提供具體的編碼實現方法,但為通信信息的研究指明了方向。香農第一定理是可變長無失真信源編碼...
