信號博弈

信號博弈（signaling game）是一種不完全信息動態博弈。典型的信號博弈包含兩名參與者：信號傳送者（sender）和信號接收者（receiver）。信號傳送者首先行動，向信號接收者傳送一個關於自身類型的信號，信號接收者收到信號後根據信號的內容選擇行動，最終雙方的收益均由信號傳送者的類型，信號傳送者選擇傳送的信號，與信號接收者的行動共同決定。

基本介紹

• 中文名：信號博弈
• 外文名：signaling game

簡介

關於信號博弈，最早的研究之一來自斯賓塞（Spence）在1973年提出的教育模型：一位工人知道自己的才能是高或低，而他的僱主不知道。工人向僱主傳送一個關於自己教育水平高低的信號，僱主收到此信號後決定給出的工資。最終工人的收益為工資減去教育成本，而教育成本由工人的才能與教育水平共同決定；僱主的收益為工人產出減去工資，而工人產出由工人的才能決定。在此模型中，信號傳送者是工人，其類型是才能高或才能低；信號接收者是僱主，其行動則是選擇給出不同的工資；信號則是教育水平高或教育水平低。

信號博弈有兩個依次進行的階段，故是動態博弈；信號博弈中信號傳送者的類型僅由傳送者自己知道，而信號接收者不知道，故是不完全信息的博弈。對於不完全信息的博弈，通常的處理方法是海薩尼轉換——引入“自然”這一第三方首先行動，以某種機率分布將不同的類型賦予信號傳送者，且這一機率分布是公共知識。這就使得博弈雙方都完全清楚博弈的所有規則，從而將博弈變為信息完全但不完美的博弈。

博弈模型

下面我們用形式化的語言描述一個最簡單的信號博弈，作為以下均衡分析的基礎。博弈包含兩名玩家，信號傳送者（記為S）與信號接收者（記為R）。S只有兩種類型：和，可以傳送兩種信號：和，R收到信號後只有兩種行動：和。博弈順序如下：

1. “自然”首先行動，以p的機率選擇S的類型為，以1-p的機率選擇S類型為；
2. S知曉自身類型後，選擇傳送信號或；
3. R接收到信號後，選擇行動或；
4. 最終S和R的收益分別為：和其中i=1，2。

均衡分析

策略類型

由上述信號博弈的簡單模型可知，信號傳送者可能有兩種類型，可以傳送兩種信號，故其有4種純策略：

1. 策略，即無論自身類型如何，都傳送信號；
2. 策略，即無論自身類型如何，都傳送信號；
3. 策略，即自身類型為時傳送信號，自身類型為時傳送信號；
4. 策略，即自身類型為時傳送信號，自身類型為時傳送信號。

依據完全類似的推理，信號接收者有4種純策略：

1. 策略，即無論收到信號如何，都選擇行動；
2. 策略，即無論收到信號如何，都選擇行動；
3. 策略，即收到信號時選擇行動，收到信號時選擇行動；
4. 策略，即收到信號時選擇行動，收到信號時選擇行動。

對於信號傳送者的1，2策略，所傳送的信號類型與自身類型無關，這類策略被稱為混同（pooling）策略；對於信號傳送者的3，4策略，不同類型的傳送者會發出不同的信號，這類策略被稱為分離（separating）策略；若傳送者的類型多於兩種，還有可能出現某一些類型的傳送者都傳送相同的信號，另一些類型的傳送者傳送不同的信號的情況，這被稱為部分混同（partial-pooling）或準分離（semi-separating）的策略。同時，某種類型的傳送者還可以隨機化自己的策略，如類型為的傳送者以p的機率傳送信號，1-p的機率傳送信號，這被稱為混合（hybrid）策略。

精煉貝葉斯均衡

對應於不完全信息動態博弈的均衡概念為精煉貝葉斯均衡（Perfect Bayesian equilibrium），它可以看作是子博弈精煉納什均衡在不完全信息條件下的自然擴展。精煉貝葉斯均衡不再是單純的策略組合，而是還需要包含參與人在進行決策時對已發生歷史的估計，這在博弈論中被稱為信念（belief）。舉例來說，信號傳送者在決定傳送什麼信號之前，對於“自然”選擇其類型為的機率p的估計就是一種信念。

對於一般的不完全信息的動態博弈，其精煉貝葉斯均衡包含兩個部分：策略組合和對應的信念系統。對於策略組合，精煉貝葉斯均衡要求每位參與人在決策時，在給定了關於此時歷史的信念之後，參與人的策略一定是對其他參與人策略的最優反應，這也被稱為序貫理性（sequential rationality）。而對於信念，精煉貝葉斯均衡常常要求下面三個附加限制：

1. 與策略的一致性（consistency with strategies）
2. 結構一致性（structural consistency）
3. 共同信念（common beliefs）

想要完全解釋這些限制的含義需要較多的背景知識，這裡不再詳述。

信號博弈作為一個較為簡單的不完全信息的動態博弈，其信息不完全之處其實只有參與人的類型，故我們可以得到一個相對簡單的均衡定義。簡單來說，信號博弈的精煉貝葉斯均衡需要滿足下面4個條件：

1. 序貫理性：每位參與人在決策時，給定了關於此時歷史的信念之後，參與人的策略一定是對其他參與人策略的最優反應；
2. 正確初始信念：每位信號接受者都對信號傳送者類型的分布具有相同的，正確的估計；
3. 行動確定的信念：只有信號傳送者的不同信號影響到信號接受者關於他類型的信念；
4. 貝葉斯更新：某位參與人在某種情形下的行動與其他參與人關於此的信念是一致的。

例子

我們來計算下面這個信號博弈的精煉貝葉斯均衡，此博弈的基本設定與簡介中的基本模型一致：

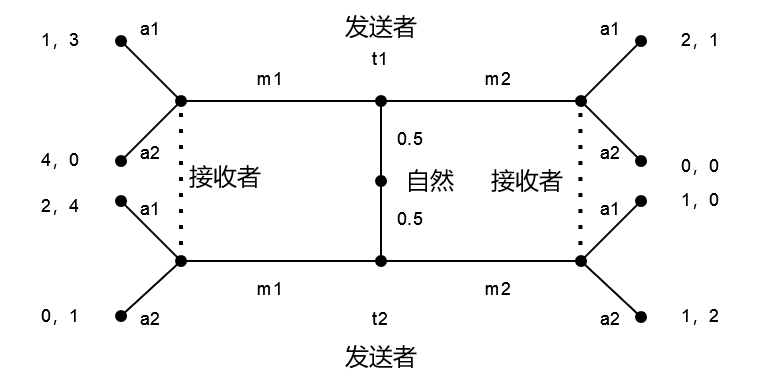
上圖示注了每一種情形下雙方的具體收益，以及自然選擇傳送者類型為，的機率均為0.5，最後不妨設信號接收者在接收到信息時認為信號傳送者的類型為以機率p為類型，機率1-p為類型；在接收到信號時認為信號傳送者的類型為以機率q為類型，機率1-q為類型，此即接收者的信念。

下面我們從信號傳送者的角度出發，依次檢查傳送者的4種純策略有哪些可能成為精煉貝葉斯均衡。

策略

此時實際上信號沒有為接收者提供額外的，能夠判斷發送者類型的信息，故其信念為p=1-p=0.5，與先驗分布相同。考慮此時接收者的最優反應：

選擇行動，則期望收益為

選擇行動，則期望收益為

顯然最優反應是，實際上由期望收益的形式可知，不論p取值如何，均是此情況下的最優反應。此時為了使得信號傳送者的最優策略是，需要不論信號傳送者類型如何，傳送信號的收益總大於傳送信號的收益。考慮到：

• 如果接收者對的反應是，那么類型為的傳送者的收益為2，嚴格大於其傳送時的收益，故類型為的傳送者不會選擇傳送；
• 如果接收者對的反應是，那么類型為和的傳送者傳送信號的收益分別為0和1，而傳送信號的收益為1和2（根據上面的分析，此時接受者會選行動），後者嚴格大於前者，故此時類型和的傳送者都會選擇傳送信號。

綜上所述，想要成為均衡，則接收者對於的反應必須是，也即此均衡下接收者的策略必須為。下面分析接收者收到信息時選擇行動是最優策略的條件：

• 選擇行動，則期望收益為
• 選擇行動，則期望收益為

故此時為最優策略的條件為也即。

故我們求得了一個精煉貝葉斯均衡：。

2. 策略

類似的，此時q=0.5，考慮此時接收者的最優反應：

• 選擇行動，則期望收益為
• 選擇行動，則期望收益為

故接收者的最優反應是。此時類型為和的傳送者收益分別為0和1。但由上面的分析可知，只要接收者收到，其最優反應就是，這意味著類型為的傳送者可保證此情況下有收益1，這一收益嚴格大於0。因此，不可能存在傳送者策略為的精煉貝葉斯均衡。

3. 策略

此時接收者在收到信號後就能完全確定傳送者的類型是還是，也即p=1，q=0。此時收到信號和時接收者的最優反應為和，且兩種情形下傳送者的收益均為1。此時成為均衡還需要成為傳送者的最優反應。然而，此時類型為的傳送者改變策略傳送，那么他的收益將為2，嚴格大於1，故不存在傳送者策略為的精煉貝葉斯均衡。

4. 策略

類似的，此時p=0，q=1，接收者的最優反應為，此時兩種類型的傳送者的收益均為2。此時成為均衡還需要成為傳送者的最優反應。可以驗證，此時類型為的傳送者改為傳送，其收益降低到1；類型為的傳送者改為傳送，其收益降低到1，故確實是此時傳送者的最優反應。即是此博弈的一個精煉貝葉斯均衡。

變體

空談博弈

在信號博弈中，傳送信號的不同確實造成了雙方收益的不同。如果信號的不同並不影響到雙方的收益（例如傳送信號是沒有成本的），雙方的收益都僅由信號傳送者的類型和信號接收者的行動決定，我們就得到了空談博弈（Cheap talk）。顯然，此時傳送者傳送信號的意義在於影響接收者對其類型的判斷，空談博弈可以看作是信號博弈的一種簡化。