低密度奇偶檢查碼

低密度奇偶檢查碼（Low-density parity-check code，LDPC code），是線性分組碼（linear block code）的一種，用於更正傳輸過程中發生錯誤的編碼方式。

基本介紹

• 中文名：低密度奇偶檢查碼
• 外文名：Low-density parity-check code
• 縮寫：LDPC code

歷史

在1962年，低密度奇偶檢查碼(LDPC code)即被Gallager提出，並被證明其錯誤校正能力非常接近理論最大值，香農極限(Shannon Limit)；不過受限於當時技術，低密度奇偶檢查碼並無法實現。低密度奇偶檢查碼被重新發現，並隨著積體電路的技術演進，低密度奇偶檢查碼的實現逐漸可行，而成為各種先進通信系統的頻道編碼標準。

運作

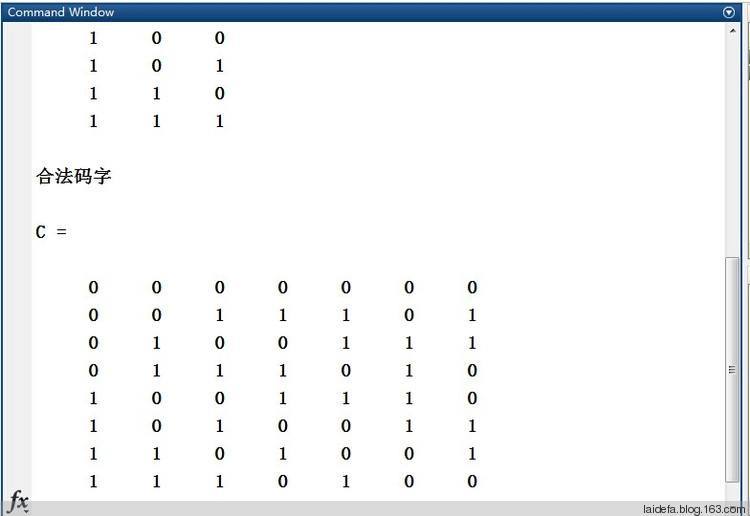
低密度奇偶檢查碼是基於具有稀疏矩陣性質的奇偶檢驗矩陣建構而成。對(n, k)的低密度奇偶檢查碼而言，每k比特數據會使用n比特的碼字(codeword)編碼。以下是一個被(16, 8)的低密度奇偶檢查碼使用的奇偶檢驗矩陣H。當中可以見得矩陣內的元素1數量遠少於元素0數量，所以具有稀疏矩陣性質，也就是低密度的由來。

解碼

低密度奇偶檢查碼的解碼，可對應成二分圖(bipartite graph)作表示。下方的二分圖是依照上述奇偶檢驗矩陣H建置，其中H的行(column)對應至check node，而H的列(row)對應至bit node。check node和bit node之間的連線，由H內的元素1決定；好比H中第一行(column)和第一列(row)的元素1，使check node和bit node兩者各自最左手邊的第一個彼此連線。

低密度奇偶檢查碼的解碼算法，主要基於有疊代性(iterative)的置信傳播(belief propagation)；整個解碼流程如下方所示：

1. 當接收數據R從通信頻道(channel)進入低密度奇偶檢查碼的解碼器，解碼器會對訊息作初始化(initialization)。
2. check node根據互相連線的多個bit node內的數據做更新運算(update)。
3. bit node對相連線的多個check node內的數據做更新運算。
4. 觀察終止(termination)條件，來決定是否繼續疊代計算。

詳細的解碼算法，常見有兩種：總和-乘積算法(Sum-Product Algorithm)和最小值-總和算法(Min-Sum Algorithm)。總和-乘積算法具有較佳的錯誤更正能力，卻具較高的計算複雜度；反之，最小值-總和算法在稍微減低的錯誤更正能力下，換取較低的計算複雜度。

總和-乘積算法

假設在一通信系統的頻道有AWGN屬性，而傳送信號為，接收信號是，bit node有n個，check node有m個。而總和-乘積算法在解碼流程如下：

初始化：假設AWGN的方差(variance)是。

bit noden會被初始化成：

。

check nodem會被初始化成：

。

check node更新：

check nodem更新為：

；其中是連線到check nodem的bit node組合，但不包含第n個bit node。

bit node更新：

bit noden更新為：

；其中是連線到bit noden的check node組合，但不包含第m個check node。

終止：

解碼比特計算：假設解碼後信號為。Hard-decision解碼比特可由下列兩式求出：

只要解碼後的碼字在恆等式成立，即終止疊代計算。

最小值-總和算法[編輯]

最小值-總和演算，大抵上和總和-乘積算法類似，除了於“check node更新”做不一樣的計算方式。而改變的計算式如下：

。