電場中某點的位移電流密度等於該點的電位移矢量對時間的變化率。
基本介紹
- 中文名:位移電流密度
- 外文名:Displacement current density
- 領域:電磁學
- 定義:電位移矢量對時間的變化率
- 相關名詞:位移電流
簡介
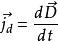
電位移矢量
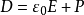
位移電流和位移電流密度的定義式
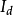
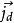

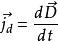

位移電流密度公式的一種導出方法
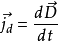
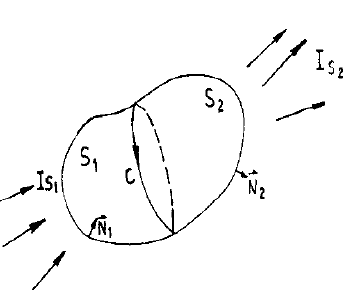
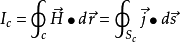
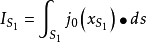

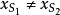
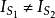
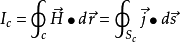
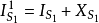
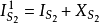
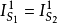
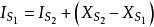
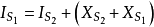
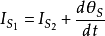
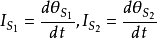
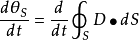
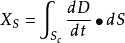
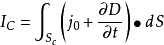
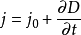
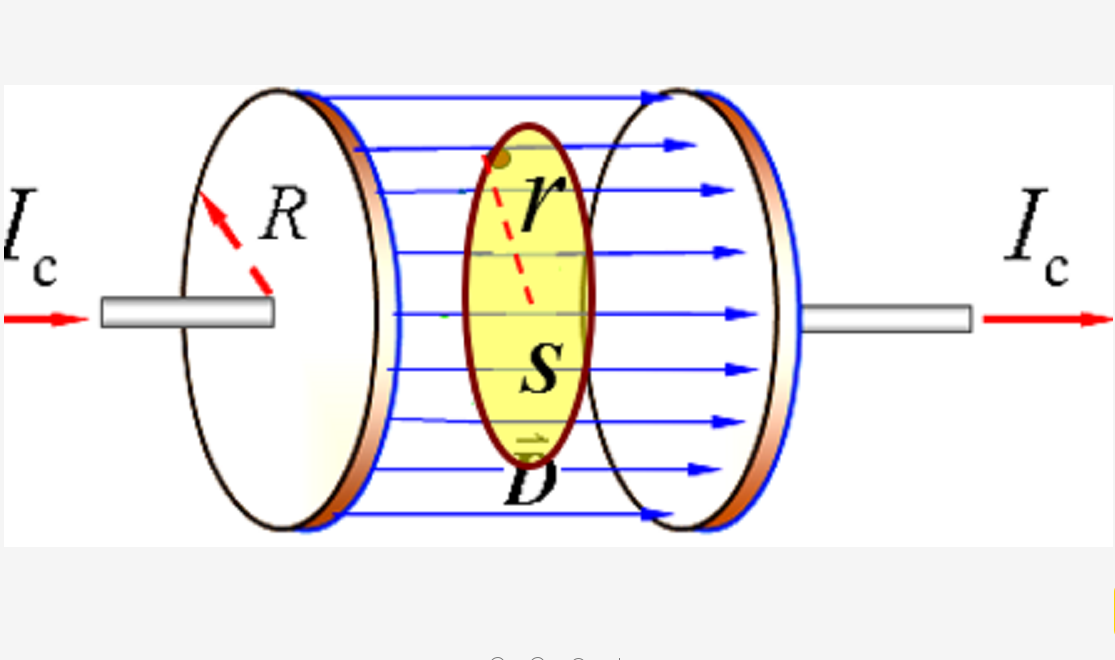
電場中某點的位移電流密度等於該點的電位移矢量對時間的變化率。
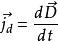
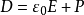
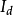
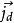

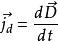

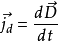

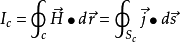

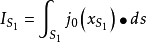

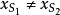
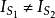
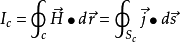
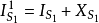
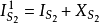
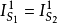
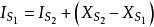
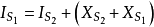
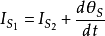
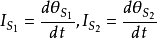
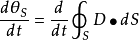
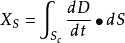
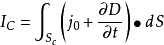
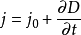
電場中某點的位移電流密度等於該點的電位移矢量對時間的變化率。...... 等於通過該截面的電位移通量的時間變化率;電場中某點的位移電流密度等於該點處電位移矢量的...
位移電流是電位移矢量隨時間的變化率對曲面的積分。英國物理學家麥克斯韋首先提出這種變化會產生磁場的假設,並稱其為“位移電流”。但位移電流只表示電場的變化率,與...
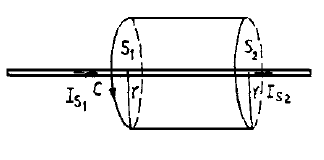
一般情形下,通過空間某截面的電流應包括傳導電流與位移電流和運流電流,其和稱全電流(total current) 。即:傳導電流Ic + 運流電流Iv + 位移電流Id = 全電流,...
在時變電磁場中,安培環路定律中的Ic應擴展為全電流,它包括傳導電流與位移電流(D)。而Jc相應地也應擴展為全電流密度J,它包括傳導電流密度與位移電流密度(圖3)。...
(4)磁場強度的旋度等於該點處傳導電流密度與位移電流密度的矢量和(麥克斯韋-安培環路定律)。詞條標籤: 科技產品 , 科學, 學科 圖集 電磁場理論圖冊 V百科往期...
麥克斯韋在穩恆場理論的基礎上,提出了渦旋電場和位移電流的概念。這就是麥克斯韋電磁場理論的基本概念如下:變化的電場和變化的磁場彼此不是孤立的,它們永遠密切地...
麥克斯韋方程組(英語:Maxwell's equations),是英國物理學家詹姆斯·克拉克·麥克斯韋在19世紀建立的一組描述電場、磁場與電荷密度、電流密度之間關係的偏微分方程。它...
麥克斯韋稱 為位移電流,即---位移電流密度 jD討論:a.引入位移電流ID,中斷的傳導電流I由位移電流ID接替,使電路中的電流保持連續b.傳導電流和位移電流之和稱為全電...
的時間變化率,即位移電流密度,其面積積分為 。磁路中磁場強度的計算公式磁場強度的計算公式:其中H為磁場強度,單位為A/m;N為勵磁線圈的匝數;I為勵磁電流(測量值)...
推廣到真空中的電場,並且認為;電位移隨時間變化也要產生磁場,因而稱一面積上電通量的時間變化率為位移電流,而電位移矢量D的時間導數(即дD/дt)為位移電流密度...
推廣到真空中的電場,並且認為:電位移隨時間變化也要產生磁場,因而稱一面積上電通量的時間變化率為位移電流,而電位移矢量D的時間導數(即дD/дt)為位移電流密度...
在時變電磁場中,電位移的時間變化率就是位移電流密度。電位移的單位在國際單位制中為庫侖/米2(C/m2)。電介質套用 在電工技術中,電介質主要用作為電氣絕緣材料,...
電磁場與帶電物體 (電荷或電流)之間的相互作用可以用麥克斯韋方程和洛倫茲力...的時間變化率為位移電流,而電位移矢量D的時間導數(即дD/дt)為位移電流密度...
