伴侶矩陣

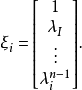
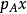伴侶矩陣亦稱友矩陣，是矩陣標準形理論中一類重要的矩陣。

基本介紹

• 中文名：伴侶矩陣
• 外文名：companion
• 適用範圍：數理科學

簡介

伴侶矩陣亦稱友矩陣，矩陣標準形理論中一類重要的矩陣。

設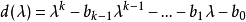 是數域 P 上的首一多項式，則 P 上的矩陣

稱為多項式 d(λ) 的伴侶矩陣。設 是 d(λ) 的友矩陣，則特徵矩陣的不變因子是1,1,...,d(λ)。

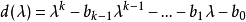
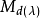
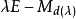
相關定理

定理1

每一個首 1 多項式既是它的友矩陣的最小多項式，又是它的友矩陣的特徵多項式。

如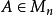的極小多項式的次數為 n ，那么與每一個特徵值對應的最大的Jordan塊就是與每一個特徵值對應的唯一的Jordan塊．這樣的矩陣是無損的，特別地，每一個友矩陣都是無損的，當然，不一定每個無損的矩陣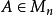都是友矩陣，但是 A 與 A 的特徵多項式的友矩陣 C 有同樣的Jordan標準型(與每一個不同的特徵值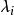對應的只有一個分塊，所以 A 與 C 相似。

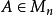
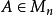
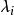
定理2

設 C 為多項式 p(x) 的友矩陣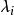，是 C 的特徵值，則

是 C 的對應於的特徵向量。

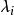
定理3

n 階複數矩陣 A 相似於它的特徵多項式的友鉅陣，當日僅當 A 的最小多項式與特徵多項式相同。

定理4

設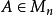有極小多項式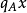以及特徵多項式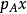，則下面諸結論等價：

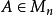
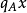
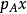
(a)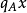的次數為n；

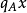
(b)=；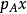

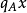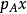
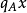
(c)A是無損的；

(d)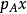與P^(t)的友矩陣相似。