伯特蘭—切比雪夫定理說明：若整數n > 3，則至少存在一個質數p，符合n < p < 2n − 2。另一個稍弱說法是：對於所有大於1的整數n，存在一個質數p，符合n < p < 2n。
基本介紹
- 中文名：伯特蘭-切比雪夫定理
- 外文名：Bertrand Chebyshev theorem
- 提出者：約瑟·伯特蘭
- 提出時間：1845年
- 套用學科：數學
- 適用領域範圍：函式
- 適用領域範圍：數學
發展簡史,驗證推導,
發展簡史
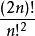
驗證推導
在證明 Bertrand 假設前我們先來證明幾個輔助命題。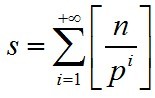
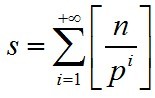
引理 1： 設 n 為一自然數， p 為一素數， 則能整除 n! 的 p 的最高冪次為：s，（[x]表示不大於x的最大整數）。
證明： 能整除 n! 的 p 的最高冪次顯然等於從 1 到 n 的各自然數中 p 的最高冪次之和， 即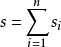 
(其中 si 為能整除 i 的 p 的最高冪次)。 然後將從 1 到 n 的所有 (n 個) 自然數排列在一條直線上， 在每個數字上疊放一列 si 個記號， 顯然記號的總數是 s。 關係式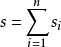表示的是先計算各列的記號數 (即 si) 再求和。 但我們也可以先計算各行的記號數再求和， 由此得到的關係式正是引理 1。為了證明這一點， 我們從數字所在的直線開始自下而上計數。很明顯所有第一行有記號的數字都含有因子 p (因為否則的話 si = 0， 沒有記號)，這種數字的總數 (也就是該行的記號總數)是 n/p ； 第二行有記號的數字都含有因子 p2 (因為否則的話 si < 2， 在第二行上不會有記號)，這種數字的總數 (也就是該行的記號總數) 是 n/p2 ，依此類推，第i行的記號總數為 n/pi 。 將所有這些數字相加便證明了引理 1。 Q.E.D. （此段冗餘 應放入“勒讓德定理”詞條 直接從推論1.1開始）
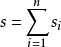
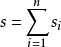
我們之所以用這樣一種比較文字化的方式來敘述引理 1 的證明過程， 目的在於更清楚地顯示該證明的基本思路：即利用一個有限二維點陣求和的不同方式 (順序) 得到互相等價的不同表達式。 這是數學證明中一種常用的手段。
推論 1.1： 設 n 為一自然數， p 為一素數， 則能整除
的 p 的最高冪次為： 
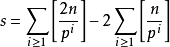
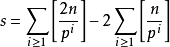
證明： 顯然。 Q.E.D.
推論 1.2： 設 n ≥ 3為一自然數， p 為一素數，s為能整除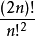
的 p 的最高冪次， 則：(a) p^s ≤ 2n； (b) 若 p > √2n，則s≤1；(c) 若 2n/3 < p ≤ n，則s = 0。
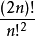
證明： (a) 設 m 為滿足 p^m ≤ 2n 的最大自然數， 則顯然對於 i > m， [2n/pi ]- 2 [n/pi ]= 0 - 0 = 0。因此推論 1.1 中的求和止於 i = m， 總計 m 項。 由於 [2x ]- 2 [x ]≤ 1， 因此這 m 項中的每一項不是 0 就是 1， 其求和結果不超過項數本身， 即 s ≤ m， 因此 p^s ≤ p^m ≤ 2n。
(b) 因為 p > √2n 表明 p^2 > 2n， 因此由 (a) 可得 s ≤ 1。
(c) 因為 n ≥ 3 及 2n/3 < p ≤ n 表明 p^2 > 2n，因此推論 1.1 中的求和只有 i = 1 一項， 即： s = [2n/p] - 2 [n/p] 。 由於 2n/3 < p ≤ n 還表明 1 ≤ n/p < 3/2， 因此 s = 2n/p - 2 n/p = 2 - 2 = 0。 Q.E.D.
引理 2： 設 n 為自然數， p 為素數， 則 Π(p≤n) p < 4^n。
證明： 用數學歸納法。 n = 1 和 n = 2 時引理顯然成立。
假設引理對 n < N 成立 (N > 2)， 我們來證明 n = N 的情形。 如果 N 為偶數， 則
，引理顯然成立。
如果 N 為奇數， 設 N = 2m + 1 (m ≥ 1)。 注意到所有 m + 1 < p ≤ 2m + 1 的素數都是組合數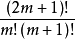 
的因子 (因為它們是 (2m+1)! 的因子， 但卻不是 m! 和 (m+1)! 的因子)； 另一方面組合數 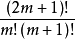在二項式展開 (1+1)^(2m+1)中出現兩次， 因而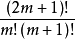
。
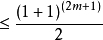
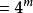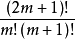
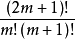
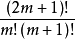
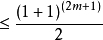
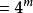
這兩點合併可得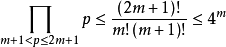
。 由此 (並利用歸納假定) 可得
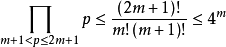
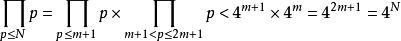
引理 2 常常被表述為
， 並被稱為 Chebyshev's Bound (以 Chebyshev 命名的結果， 無論是前面提到的 Bertrand 假設的別稱 Chebyshev 定理還是這裡所說的 Chebyshev's Bound， 都有不止一個對應， 查閱文獻時要當心)。
好了，一切準備就緒，然後我們來證明 Bertrand 假設。
Bertrand 假設的證明：
用反證法， 假設命題不成立，即存在某個 n ≥ 2， 在 n 與 2n 之間沒有素數。 我們來看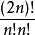
的分解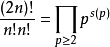
(s(p)為質因子 p 的冪次)。 由推論 1.2(a) 知 p < 2n， 由反證法假設知 p ≤ n， 再由推論 1.2(c) 知 p ≤ 2n/3，因此 (2n)!/(n!n!) = Πp≤2n/3 ps(p)。 將連乘分解為 p ≤ √2n 及 √2n < p ≤ 2n/3 兩部分 (這一分解要求 n > 4， 但後面我們會看到， 我們的整個方法只適用於 n ≥ 50， 因此我們其實是假定 n ≥ 50， 對 50 以下的情形只需直接驗證即可)， 並利用推論 1.2(b) 可得：
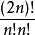
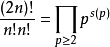
(2n)!/(n!n!) ≤ Πp≤√2n ps(p) · Π√2n p ≤ Πp≤√2n ps(p) · Πp≤2n/3 p
該乘積中的第一組的被乘因子數目為 √2n 以內的素數數目，即不多於 √2n/2 - 1 (因偶數及 1 不是素數)， 而每個因子按照推論 1.2(a) 均不大於 2n， 因此該組乘積不大於 (2n)√2n/2-1。 第二組乘積按照引理 2 小於 42n/3， 由此得到：
(2n)!/(n!n!) < (2n)√2n/2-1 · 42n/3。
另一方面， (2n)!/(n!n!) 是 (1+1)2n 展開式中最大的一項， 而該展開式共有 2n 項 (我們將首末兩項 1 合併為 2)， 因此 (2n)!/(n!n!) ≥ 22n / 2n = 4n / 2n。將此式與上一段最後的結果聯立並略經化簡可得 4n/3 < (2n)√n/2。兩端取對數並進一步化簡可得：
√2n ln4 < 3 ln(2n)
由於冪函式 √2n 隨 n 的增長速度遠快於對數函式 ln(2n)， 因此上式對於足夠大的 n 顯然不可能成立。簡單的數值計算表明， 對於 n = 50 上式左邊為 13.8629...， 右邊為 13.8155...， 不等式不成立。 這表明我們所作的反證假設， 即 Bertrand 假設不成立， 對於 n ≥ 50 是錯誤的， 換句話說 Bertrand 假設對於 n ≥ 50 成立。 簡單的驗證可以證明 Bertrand 假設對於 n < 50 也成立 (事實上前面說過，Bertrand本人就已經對 n < 3000000 做過驗證)， 因此我們證明了 Bertrand 假設。 Q.E.D.
由於本文是本系列文章的第一篇，在這裡稍稍說上幾句題外話。 對於沒有從事過研究工作的人來說，複雜數學定理(Bertrand 假設當然不在此列)的證明常常顯得有些高深莫測。一個具有足夠理解力和適當基礎的人也許可以看懂一個複雜證明的每一個推理環節，但一環環地攀完了長長的邏輯鏈條後仍不免有一種 “只見樹木， 不見森林”的感覺。那些幽深曲折，有時甚至是匪夷所思的精巧思路委實讓人驚嘆不已。那些精巧思路的一部分是來源於經年累月的嘗試和努力，就象小時候很多人愛玩的畫報上的迷宮遊戲，一次次碰壁，一次次重來，才換得最後那條精巧的勝利折線。局外人只看結果，自不免驚為神來之筆。不過這類比擬不可無限外推，讓人誤以為只要敢於嘗試，不怕碰壁，就一定能夠成功。須知人力有時而窮，一味地相信“人定勝天”並不是科學的態度。數學世界不是畫報上的迷宮，畫報上的迷宮是有限的，數學世界的變化卻是無窮的。數學是一門大智慧的學問，絕非是只憑苦力就一定能夠換取成功的。如果一味地蠻幹，甚至是只學了一點初等數學就迫不及待地企圖用自己的勤奮來攻克最艱深的數學問題，則往往窮盡一生一世也只是枉費心力，且有可能走火入魔。
重新回到 Bertrand 假設上來， Bertrand 假設是一個非常簡單的定理， 本文所介紹的證明其基本思路在於顯示當 n 與 2n 之間不存在素數時 (2n)!/(n!n!) 將無法找到足夠多的素數因子來作分解， 也就是說 (2n)!/(n!n!) 的素數分解表達式將小於 (2n)!/(n!n!)，這就是上面不等式無法成立的原因。 為什麼選 (2n)!/(n!n!) 作為分析的對象？ 那是因為 (2n)!/(n!n!) = (n+1)···(2n)/n! 包含了所有 n 與 2n 之間的素數因子 (分子上的 (n+1)···(2n))，而又很聰明地約去了許多小於 n 的素數因子 (分母上的 n!)，因此非常適合於用來顯示缺少了 n 與 2n 之間的素數所造成的後果。
Bertrand 假設對素數分布作了非常粗略的描述，它表明在x附近的素數分布密度至少是 1/x。與素數定理給出的1/ln(x)相比，Bertrand假設給出的顯然很粗略(不過素數定理給出的密度是平均意義上的，而Bertrand 假設給出的是嚴格的密度下界)，因而存在加強的餘地。在本文的最後我們列舉其中兩個這樣的加強結果(定理)：
定理 1： 對任意自然數 n > 6， 至少存在一個 4k + 1 型和一個 4k + 3 型素數 p 使得 n < p < 2n。
定理 2： 對任意自然數 k， 存在自然數 N， 對任意自然數 n > N 至少存在 k 個素數 p 使得 n < p < 2n。
