實際數(practical number)是指一正整數n有許多約數,所有小於n的正整數都可以用數個n的相異真約數和表示。
基本介紹
- 中文名:實際數
- 外文名:practical number
- 領域:統計學
簡介
實際數的充份必要條件



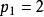

和其他數列的關係
和埃及分數的關係
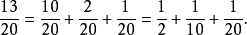
實際數(practical number)是指一正整數n有許多約數,所有小於n的正整數都可以用數個n的相異真約數和表示。



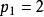

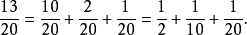
實際數(practical number)是指一正整數n有許多約數,所有小於n的正整數都可以用數個n的相異真約數和表示。...
實際參數簡稱“實參”。在調用有參函式時,函式名後面括弧中的參數稱為“實際參數”,實參可以是常量、變數或表達式。...
數量差異亦稱用量差異,產品耗用資源的實際數量與標準數量之差與標準價格的乘積。...... 數量差異亦稱用量差異,產品耗用資源的實際數量與標準數量之差與標準價格的乘積...
主要應檢查的問題有:有無轉移銷售收入;有無應作銷售未計銷售;有無用應稅產品兌換原材料、固定資產等少計銷售的情況;按加工產品綜合回收率,將加工精選煤實際數量...
一個能表示原來物體或事件的實際數量的數,這個數稱為準確數。與近似數相對。準確數:與實際完全符合的數,近似數:與實際接近的數,該學案主要內容包括教學目標、教學...
理論頻數又稱驗頻數,統計學概念,是指用陽性理論率推算各實際頻數的估計值 。...... 理論頻數又稱驗頻數,統計學概念,是指用陽性理論率推算各實際頻數的估計值 。...
累計數指標:指一個時期的實際數據之和。如“十一五”累計基礎設施投資總額,即為2006、2007、2008、2009、2010年五年之和。1 ...
標準成本差異是指產品的實際成本與產品的標準成本之間的差額。...... 直接人工成本差異是指直接人工實際成本與標準成本之間的差額。其也被分為價格差異和數量差異。其...
所謂成本差異是指產品實際成本與標準成本的差額。實際成本超過標準成本所形成的差異稱為不利差異(Adverse variance),通常用字母A來表示;實際成本小於標準成本所形成的...
數學與套用數學(Mathematics and Applied Mathematics)是一個學科專業,該專業培養掌握數學科學的基本理論與基本方法,具備運用數學知識、使用計算機解決實際問題的能力,...
積數計息法就是按實際天數每日累計賬戶餘額,以累計積數乘以日利率計算利息的方法。...... 積數計息法就是按實際天數每日累計賬戶餘額,以累計積數乘以日利率計算利息...
比較對照是人們認識客觀事物時普遍使用的一種邏輯思維方法,是統計綜合分析研究中最常用的一種有效方法。所謂統計比較,是將統計指標所反映的實際數量狀況與有關標準...
卡方檢驗就是統計樣本的實際觀測值與理論推斷值之間的偏離程度,實際觀測值與理論...自由度v=(行數-1)(列數-1)=12. 套用條件:要求樣本含量應大於40且每個...
即按照數學內部的需要,或未來可能的套用,對數學結構本身的內在規律進行研究,而並不要求同解決其他學科的實際問題有直接的聯繫,只是以純粹形式研究事物的數量關係和...
移動平均法是用一組最近的實際數據值來預測未來一期或幾期內公司產品的需求量、公司產能等的一種常用方法。移動平均法適用於即期預測。當產品需求既不快速增長也不...
不良數管制圖又稱np圖,np圖用來度量一個檢驗中的不良品(不合格品) 的數量。與p圖(b)不同,np圖表示不合格品的實際數量而不是與樣本的比率。np管制圖的套用...
數量變動影響金額=實際價格×實際數量-實際價格×預算數量=實際價格×數量差異 價格變動影響金額=實際價格×實際數量-預算價格×實際數量=價格差異×實際數量 (2)連環...
盤點是指定期或臨時對庫存商品實際數量進行清查、清點的一種作業。...... 1.貨物數量通過點數計數查明商品在庫的實際數量,核對庫存賬面資料與實際庫存數量是否一致。...
1 實際天數/實際天數 2 實際天數/360 3 實際天數/365 4 歐洲30/360 註解Microsoft Excel可將日期存儲為可用於計算的序列數。默認情況下,1900年1月1日的...
直接材料成本差異是指為完成實際產量或作為量所消耗的直接材料按實際成本計算與按標準成本計算之間的差額。...
