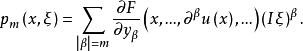仿線性化

仿線性化是對於非線性函式F(x,y)進行線性化，使其成為仿積與具更高正則性餘項之和的方法。

基本介紹

• 中文名：仿線性化
• 外文名：paralinearization
• 適用範圍：數理科學

簡介

仿線性化是對於非線性函式F(x,y)進行線性化，使其成為仿積與具更高正則性餘項之和的方法。

設F(x,y)是Rⁿ×R^N上的C^∞函式，x=(x₁,x₂,...,x_n)∈Rⁿ，y=(y₁,y₂,...,y_n)∈R^N，且它的各階導數在K上有界，K為Rⁿ×R^N中的任意緊集，則對實u^j(x)=C^ρ(Rⁿ)(p>0,j=1,2,...,N)，有

其中R(x)∈C^2ρ(Rⁿ)。又若u^j(x)∈H^s(Rⁿ)(s>n/2)，則。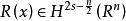

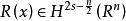
上述結果表明，對非線性函式F(x,y)可用上述一種特殊的線性化方法化成仿積及正則性更高的餘項之和。這種線性化方法稱為仿線性化。

套用

在處理具體問題時還可出現各種不同的仿線性化形式。利用上述仿線性化，可以將非線性微分方程經過線性化而用仿微分運算元來表示。

實例

考察m階完全非線性微分方程F(x,u,...,∂^βu,...)_|β|≤m=0。設F關於它的自變數為C^∞。記N為上述β取遍|β|≤m的全體的個數。設F及各階導數在緊集K⊂Rⁿ×R^N上有界。又設u(x)是方程的C^ρ+m實解，ρ>0（或H^s+m,s>n/2），則用上述仿線性化可將方程化為Pu=R(x)。此處R(x)∈C^2ρ（或H^2S-n/2），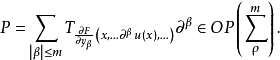

它的主象徵是

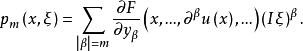當方程為擬線性或半線性時，u(x)的光滑性可減弱，R(x)的光滑性可提高。這樣非線性微分方程問題就歸結為仿微分方程的問題了。