基本介紹
數學定義,尺規作圖,推廣拓展,分數與根式,特殊的數列,黃金三角形,發展簡史,套用實例,
數學定義
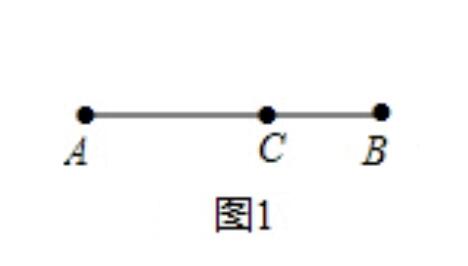
把一條線段分割為兩部分,使較大部分與全長的比值等於較小部分與較大的比值,則這個比值即為黃金分割。其比值是(√5-1):2,近似值為0.618,通常用希臘字母Ф表示這個值。
附:黃金分割數前面的32位為:0.6180339887 4989484820 458683436565
 | 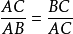 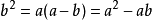 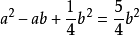 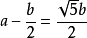 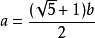 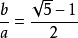 |
尺規作圖
1、設已知線段為AB,過點B作BD⊥AB,且BD=AB/2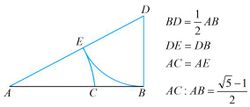 圖示
圖示
 圖示
圖示2、連結AD
3、 以D為圓心,DB為半徑作弧,交AD於E
4、以A為圓心,AE為半徑作弧,交AB於C,則點C即為黃金分割點
在一個黃金矩形中,以一個頂點為圓心,矩形的較短邊為半徑作一個四分之一圓,交較長邊於一點,過這個點,作一條直線垂直於較長邊,這時,生成的新矩形仍然是一個黃金矩形,這個操作可以無限重複,產生無數個的黃金矩形。
推廣拓展
分數與根式
特殊的數列
設一個數列,它的最前面兩個數是1、1,後面的每個數都是它前面的兩個數之和。例如:1,1,2,3,5,8,13,21,34,55,89,144·····這個數列為“斐波那契數列”,這些數被稱為“斐波那契數”。
經計算發現相鄰兩個斐波那契數的比值是隨序號的增加而逐漸逼近黃金分割比。由於斐波那契數都是整數,兩個整數相除之商是有理數,而黃金分割是無理數,所以只是不斷逼近黃金分割。
黃金三角形
所謂黃金三角形是一個等腰三角形,其底與腰的長度比為黃金比值,正是因為其腰與邊的比為(√5-1)/2而被稱為黃金三角形。黃金分割三角形是唯一一種可以用5個而不是4個與其本身全等的三角形來生成與其本身相似的三角形的三角形。由五角形的頂角是36度可得出黃金分割的數值為2sin18度(即2*sin(π/10))。
將一個正五邊形的所有對角線連線起來,在五角星中可以找到的所有線段之間的長度關係都是符合黃金分割比的,所產生的五角星裡面的所有三角形都是黃金分割三角形。
發展簡史
公元前4世紀,古希臘數學家歐多克索斯第一個系統研究了這一問題,並建立起比例理論。他認為所謂黃金分割,指的是把長為L的線段分為兩部分,使其中一部分對於全部之比,等於另一部分對於該部分之比。而計算黃金分割最簡單的方法,是計算斐波那契數列1,1,2,3,5,8,13,21,...第二位起相鄰兩數之比,即2/3,3/5,5/8,8/13,13/21,...的近似值。


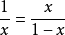
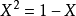

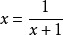
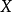
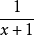
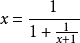
 畢達哥拉斯
畢達哥拉斯