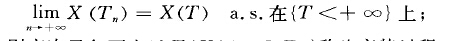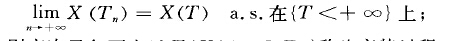亨特過程(Hunt process)是一類滿足某些連續性條件的強馬爾可夫過程。
馬爾可夫過程是一類重要的隨機過程：在已知它目前的狀態(現在)的條件下，它未來的演變(將來)不依賴於它以往的演變(過去)。這種已知“現在”的條件下，“將來”與“過去”獨立的特性被稱為馬爾可夫性，具有這樣性質的隨機過程叫做馬爾可夫過程。
基本介紹
- 中文名：亨特過程
- 外文名：Hunt process
- 領域：數學
- 性質：強馬爾可夫過程
- 本質：重要的隨機過程
- 重要理論：位勢理論
概念,馬爾可夫過程,強馬爾可夫過程,位勢理論,布朗運動,
概念
亨特過程(Hunt process)是一類滿足某些連續性條件的強馬爾可夫過程。如果下列三個條件成立：
1.它是右連續的；
2.它具有強馬爾可夫性；
3.它是擬左連續的，即對任一列上升趨於停時T的停時{Tn}，有：
則齊次馬爾可夫過程{X(t)，t∈R+}稱為亨特過程。
亨特過程與位勢理論有著密切聯繫，這種聯繫是由亨特(Hunt，G.A.)等人在把布朗運動與位勢的聯繫推廣到一般馬爾可夫過程時發展起來的。
馬爾可夫過程
馬爾可夫過程是一類重要的隨機過程：在已知它目前的狀態(現在)的條件下，它未來的演變(將來)不依賴於它以往的演變(過去)。這種已知“現在”的條件下，“將來”與“過去”獨立的特性被稱為馬爾可夫性，具有這樣性質的隨機過程叫做馬爾可夫過程。它的原始模型馬爾可夫鏈，最初由俄國數學家馬爾可夫於1907年提出。1931年原蘇聯數學家柯爾莫戈羅夫發表了《機率論的解析方法》，首先將微分方程等分析方法用於馬爾可夫過程，做了這類過程理論的奠基性工作。1951年前後，日本數學家伊藤清在法國數學家萊維和原蘇聯數學家伯恩斯坦等人工作的基礎上，建立了隨機微分方程理論，為研究馬爾可夫過程開闢了新的途徑。1954年前後，南斯拉夫—美國數學家費勒將泛函分析中的半群方法引入馬爾可夫過程的研究中，原蘇聯數學家登金等賦予它機率意義。20世紀50年代初，美國數學家J.L.杜布等發現了布朗運動與偏微分方程論中狄利克雷問題的關係，後來G.A.亨特研究了相當一般的馬爾可夫過程與位勢的關係。目前，流形上的馬爾可夫過程、馬爾可夫場等都是正待深入研究的領域。此外，中國—美國數學家鐘開萊、中國數學家王梓坤等人對馬爾可夫過程的研究很有特色，發展和建立一些新的理論和方法。
強馬爾可夫過程
強馬爾可夫過程是一類隨機過程。指具有比馬爾可夫性更強的條件無後效性的隨機過程。如果對於任意停時τ和B∈σ(X(τ+u)，u≥0)(τ後σ代數)，有：
其中Fτ={A∈F，A∩{τ≤t}∈Ft}是τ前σ代數，則稱馬爾可夫過程{X(t)，t∈R+}是強馬爾可夫過程。由等式(1)刻畫的性質稱為強馬爾可夫性。因為任意非負常數t都是一個停時，所以(1)式是“馬爾可夫過程”中性質2的加強(參見“馬爾可夫過程”)，而強馬爾可夫性只不過是在描述馬爾可夫性的等式中用任意停時τ代替任意固定的時刻t。
許多常見的馬爾可夫過程，例如，離散時間參數馬爾可夫過程，布朗運動等都具有強馬爾可夫性。但也存在馬爾可夫過程不是強馬爾可夫過程的例子。
指這樣一種隨機過程，在已知它目前狀態(現在)條件下，它未來的演變(將來)不依賴於它以往的演變(過去)。這種已知“現在”的條件下，“將來”與“過去”無關的特性稱為馬爾可夫性。其中，“現在”是指固定時刻。但實際問題中常需將馬爾可夫性中的“現在”這個時刻概念推廣為停時。直觀上講，停時是描述某種隨機現象發生的時刻，它是普通時間變數的隨機化。例如，考察從圓心出發的平面上的布朗運動，要研究首次到達圓周的時刻t以前的事件和以後的事件的條件獨立性，這裡的t就是停時，並認為t是“現在”。這種把“現在”推廣為停時情形的“現在”，且在已知“現在”的條件下，“將來”與“過去”無關的特性被稱為強馬爾可夫性。具有此性質的馬爾可夫過程稱為強馬爾可夫過程。以前，許多人認為馬爾可夫過程必然是強馬爾可夫過程。直到1956年，才有人找到馬爾可夫過程不是強馬爾可夫過程的例子。馬爾可夫過程理論的進一步發展表明，強馬爾可夫過程才是馬爾可夫過程的真正研究對象。
位勢理論
位勢的概念來源於物理學中的萬有引力理論。集中在z點的單位質量在另一點x處的位勢等於距離|z-x|的倒數。因此位勢在不分布質量的地方是x的調和函式。一般質量分布的位勢用積分表示。
源於物理學的位勢概念經許多數學家的努力形成了抽象的位勢理論，這是複變函數的理論與套用相互交融的一個最吸引人的例證。19世紀中葉以來，位勢理論逐漸成為複變函數研究的一部分。
早期的重要結果是由法國數學家泊松和英國數學家格林取得的，繼而在1840年由德國數學家高斯完成了奠基性工作。其中最重要的是邊值問題，即在一區域內決定一調和函式，使得它在邊界的極限值與一給定的函式相同。高斯的工作不夠嚴格也不夠精確，直到1900年前後才被希爾伯特嚴格地解決。以後許多數學家研究了不同的方程以及不同形式的邊界問題。
位勢理論第二個發展時期的特徵是引進測度、積分與容量的更廣的概念。這時主要研究更一般的積分：
其中N是核，μ是測度。
第三個時期大致是1940—1955年，其特點是把拓撲學套用到位勢理論中。這時測度被看作空間的一個點，它與原點的距離等於對應於該測度的能量的平方根。這樣一來就可以套用希爾伯特空間理論所常用的方法。這一時期最顯著的例子是馬丁邊界的引入。馬丁的工作激勵了法國數學家肖凱對緊凸集的極值點的深刻研究，這是20世紀中葉之後分析數學的最大發現之一。
1955年以後，除了拓撲方面的進一步改進外，又產生了位勢理論的公理化以及機率論與位勢理論的相互促進，這方面的工作主要是美國數學家杜布和亨特完成的。
布朗運動
懸浮在氣體、液體中的微小顆粒(稱為布朗粒子)受到周圍作熱運動的氣、液分子不平衡的碰撞而發生的永不停息的、不規則的運動。圖中是在顯微鏡下對懸浮在空氣中的一顆粉塵微粒每隔一秒鐘位置變化所作的記錄。顆粒越小，溫度越高，這種運動越激烈。
1827年英國植物學家布朗在顯微鏡下觀察懸浮在水中的花粉時，首先發現了這種運動，開始布朗懷疑這是由於花粉有生命造成的，於是布朗把花粉浸在酒精中將它殺死，乾枯後再作實驗，結果花粉顆粒同樣運動，他又把玻離碎片碾成細粉來作實驗，得到同樣的結果，人們又懷疑布朗粒子的運動是不是由於外界的影響(如振動、氣體或液體的對流等)引起的?精確的實驗表明：在排除外界干擾的情況下，布朗運動仍然存在。當時布朗雖不能解釋這種運動的原因，但他如實的作了詳細記錄，直到布朗逝世後，隨著氣體動理論的發展，人們才認識到布朗運動的實質：由於布朗粒子非常小，在任一瞬時，周圍分子從各方向的碰撞作用力是不平衡的，存在一個淨作用力，這個力大小、方向不斷變化，故使布朗粒子作永不停息的、無規則的運動。布朗的實驗是歷史上第一次間接顯示分子運動的著名實驗，為紀念布朗對科學的偉大貢獻，人們把這種運動命名為布朗運動。
經過70多年，到1905年，德國物理學家愛因斯坦在《物理學年鑑》第4編17卷上發表的“熱的分子運動論所要求的靜液體中懸浮粒子的運動”的論文中，從能均分定理出發，首先得出了布朗運動的完整的理論。同一時期波蘭物理學家馬·馮·斯莫盧霍夫斯基對這一課題也作了理論上的研究，法國物理學家讓·佩蘭於1908年完成了布朗運動的定量實驗。這是物質分子-原子論、氣體動理論的巨大成功，也對漲落理論的建立起了重要作用。同時，這種把原來看不見的分子的微觀運動和可以看得見的粒子的巨觀運動聯繫起來的作法，為研究物理現象提供了一種重要方法。
