亨澤爾引理(Hensel's Lemma )是代數數論中的一個重要定理。
基本介紹
- 中文名:亨澤爾引理
- 外文名:Hensel's Lemma
- 範疇:代數
由多項式在剩餘類域上的分解得出其在完備域上分解的定理.設域F,對非阿基米德賦值甲完備,O為賦值環,P為賦值理想,F=O/P.自然同態。--> F誘導出環同態O[x]~萬[x],以了(x)記f.(x)E0[x]的像.若在F[二]中有分解式了(x)=G(x)H(x)}0,式中CT(x)與H(x)為F [.x ]中互素多項式,則亨澤爾引理斷言:存在g(x),h(x)EO[x],使得f(x)=}(x))h(x),且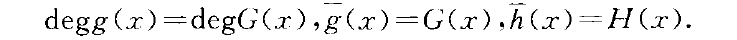
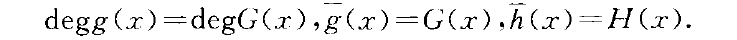
亨澤爾引理
特別地,若REF是f.(x)的單根,則存在f(x)的根bE0使b=R.由此引理知,若f(x)EO[x]首一,且在完備域F,上不可約,則.廠(x)一(U(x)”是F[x]中不可約多項式G(x)的冪.
