亞歷山大多項式

亞歷山大多項式(Alexander polynomial)扭結型的比扭結群更加易於計算的不變數。

在數學中，亞歷山大多項式是一個結不變數，它為每個結類型分配一個具有整數係數的多項式。詹姆斯·沃德爾·亞歷山大二世在1923年發現了這個第一個結多項式。1969年，約翰·康威展示了這個多項式的一個版本，現在稱為亞歷山大·康威多項式，可以用一個絞合關係來計算，儘管它的意義直到瓊斯多項式的發現。在康威重修亞歷山大多項式之後不久，人們就意識到亞歷山大的論文中關於他的多項式展示了類似的串聯關係。

基本介紹

• 中文名：亞歷山大多項式
• 外文名：Alexander polynomial
• 學科：數理科學
• 屬性：結不變數

定義

設K是三球中的一個結。讓X是無限循環蓋的的結補的ķ。此覆蓋物可以通過切割結補體沿獲得塞弗特表面的ķ並與邊界所得歧管的無窮多拷貝粘合在一起以循環的方式。在X上有一個覆蓋變換t。考慮X的第一個同源性（用整數係數）表示 。轉化t作用於同源性，所以我們可以考慮 一個模組結束 。這被稱為亞歷山大不變或亞歷山大模組。

亞歷山大證明，亞歷山大的理想是非零的，總是主要的。因此亞歷山大多項式總是存在的，顯然是一個結不變數 。僅由一個字元串配置的結的亞歷山大多項式是t的多項式，然後對於鏡像結是相同的多項式。也就是說，它不能區分結和鏡像之間的結。

計算多項式

JW Alexander在他的論文中給出了計算Alexander多項式的以下過程。

以n個交叉點為結點的方向圖； 結點圖有n+ 2個區域。要制定亞歷山大多項式，首先必須創建一個大小為（n，n+ 2）的關聯矩陣。所述N行對應於N道口，並且N+ 2列的區域。矩陣條目的值是0,1，-1，t，-t。

考慮與特定區域和交叉口相對應的條目。如果該區域不與交叉口相鄰，則該條目為0.如果該區域與交叉口相鄰，則條目取決於其位置。下表給出了從入境下交叉線的角度確定的該區域在該過境點的位置的入口。

• 在交叉之前的左邊： -t
• 在交叉前右邊：1
• 下交叉後左邊：t
• 下交叉後右邊：-1

除去從矩陣對應於相鄰區域的兩列，並制定出新的行列式Ñ通過Ñ矩陣。根據刪除的列，答案將不同乘以 。為了解決這個模糊問題，把t的最大可能冪除以-1，必要時乘以-1，這樣常數項是正的。這給了亞歷山大多項式。

亞歷山大多項式也可以從Seifert矩陣中計算出來。

亞歷山大·福克斯（Alexander R. Fox）的作品被認為是結團的共同表現 並引入了非交換微分運算元Fox（1961），它也允許計算 。有關更高亞歷山大多項式的這種方法的詳細論述可以在Crowell&Fox（1963）一書中找到。

多項式的基本屬性

亞歷山大多項式是對稱的： 為所有結K.

從定義的角度來看，這是龐加萊二元同構的表現 哪裡 是分數場的商 通過，被認為是 模組，在哪裡 是共軛 模組 即：作為一個交換團體，它是相同的 而是涵蓋了轉型行事 。

並以1：1為單位進行評估。 。

從定義的角度來看，這是一個表現，結補是由覆蓋變換產生的同源圓 。更普遍如果是一個三維流形 它有一個亞歷山大多項式定義為其無窮循環覆蓋空間的階理想。在這種情況下是等號的，等於扭力子群的順序 。

眾所周知，每一個對稱的積分Laurent多項式都是1的單位，是一個結的亞歷山大多項式（Kawauchi，1996）。

多項式的幾何意義

由於亞歷山大的理想是主要的， 若且唯若結組的換向器子組是合適的（即等於它自己的換向器子組）。

對於拓撲切片結，亞歷山大多項式滿足Fox-Milnor條件哪裡是一些其他的積分Laurent多項式。

亞歷山大多項式的次數限制結類的兩次。

麥可·弗里德曼（Michael Freedman）證明，3球體中的結是拓撲切片;即如果結的亞歷山大多項式是平凡的（Freedman和Quinn，1990），則在4球中限定一個“局部平坦”的拓撲盤。

考夫曼（Kauffman，1983）描述了從物理模型導出的亞歷山大多項式經由狀態和的第一次構造。考夫曼（Kauffman，2001）對這些話題以及與物理學的其他關係進行了調查。

還有其他的表面和平滑的四維拓撲關係。例如，在某些假設下，通過進行一個手術來修改一個光滑的四維流形，包括去除一個二維圓環的一個鄰域，並用一個與S交叉的結補代替它。結果是一個光滑的四維流形同構於原始的，但是Seiberg-Witten不變數已經被與結的亞歷山大多項式相乘而修改。

已知具有對稱性的節點具有受限的亞歷山大多項式。（Kawauchi 1996）中的對稱部分。儘管如此，亞歷山大多項式可能無法檢測到一些對稱性，如強可逆性。

如果節點補足了圓上的光纖，那么結的亞歷山大多項式就是已知的monic（最高和最低階項的係數等於）。其實，如果是一個纖維束在哪裡 是結的補充，讓表示單值，然後哪裡 是同源性的誘導圖。

亞歷山大 - 康韋多項式

亞歷山大證明了亞歷山大多項式滿足一個絞合關係。約翰·康威後來以不同的形式重新發現了這一點，並表明絞線關係和對結的價值選擇足以確定多項式。Conway的版本是一個z整數係數的多項式，表示為並稱為Alexander-Conway多項式（也稱為Conway多項式或Conway-Alexander多項式）。

假設我們有一個定向連結圖，其中 是如圖1中所示，通過交叉和平滑圖的特定交叉點的局部區域上的變化而產生的連結圖。

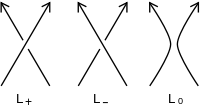
圖1

這裡是康威的關係：

（其中O是Unkn的任何圖）

與標準亞歷山大多項式的關係由下式給出 。這裡 必須正確地歸一化（乘以）來滿足絞線關係 。注意這個關係在t給出了一個Laurent多項式。

計算三葉草的Conway多項式的例子見結理論。

與Floer同源性的關係

Ozsvath&Szabo（2004）和Rasmussen（2003）使用偽全純曲線將一個稱為結Floer同源性的bigraded abel組聯繫到每個同位素結的類。結Floer同源的分級歐拉特徵是亞歷山大多項式。而亞歷山大多項式給出了一個結的下界，Ozsvath&Szabo（2004b）證明結Floer的同源性檢測到該屬。類似地，雖然亞歷山大多項式阻礙了一個在結點附近的結補體纖維化，但是Ni（2007）表明Floer的同源性完全決定了當一個結補體纖維在圓上。結Floer同源群是Heegaard Floer同源性不變族的一部分;參見Floer同源進一步討論。