變化
五階魔方總共有8個角塊、36個邊塊(兩種類型)和54箇中心塊(48塊可以移動,6塊固定)。
 五階魔方結構圖
五階魔方結構圖角塊的變化狀態和
二階魔方相同,所以總共有
種變化狀態。
五階魔方的中心塊為3×3結構,所以其每種顏色都有4中心塊是等價的,即中心塊的變化狀態為
種。
其24個外側邊塊的位置不能隨意移動,所以總共有
種變幻狀態。12箇中心邊塊中有11個可以互換位置,所以總共有
種變化狀態。
即282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000種變化狀態。
術語
五階魔方各層的表示方法:
U:上層
u:上數第二層
D:下層
d:下數第二層
L:左側層
l:左數第二層
R:右側層
r:右數第二層
F:前層
f:前數第二層
B:後層
b:後數第二層
還原方法
降階法
對於已掌握了
三階魔方還原的初學者來講,五階魔方一般可採用“降階法”還原,即將五階魔方“降階”成為三階魔方,再按三階魔方還原。
第一步,合併中心塊。 | |
第二步,合併棱邊。此時五階魔方已“降階”為三階魔方。 | |
第三步,按照三階魔方還原。 | |
層先法還原
本教程介紹的是
層先法,有興趣學習降階法的請進入五階魔方高級玩法教程頁面學習。
本解法的流程為: 第一層-----第二、三層----第四、五層, 在閱讀解法之前,請先看一下以下關於
旋轉各面的代號:
以上皆為轉90度。如果加了一個「2」,如「L2」,即為L轉180度。
對於每一面,本解法用以下的代號來指稱:
邊:Edge (Ed) 翼:Wing (W) 角:Corner (Co)
叉:Cross (Cr) 點:Point (P) 心:Center (C)
復原第一層
在解第一層時,同時要將「第一面」和「第一圈」轉正確。解法不難,以3階魔方的經驗為基礎即可輕易解決。
復原第二、三層
2.1. 復原第二層的叉(Cr)
如果在第四層找不到可用的Cr,可用公式(2-5)、(3-1)等,將可用的Cr轉到第四層。
公式2-1----F2 u' F2
2.2. 復原第二層的翼(W)
 五階魔方
五階魔方視之為3階魔方I
如果在第五層找不到可用的W,可用公式(2-2)、(3-1)等,將可用的W轉到第五層。 鏡射情形請自行想
公式2-2----U F U' F' L F' L'
2.3. 復原第三層的邊(Ed)
與(2-2)類似,只是視之為3階魔方II。
如果在第五層找不到可用的Ed,可用公式(2-3),將可用的Ed轉到第五層。 鏡射情形請自行想像。
公式2-3----Uu Ff U'u' F'f' Ll F'f' L'l' Ff
2.4. 復原第二層的點(P)
如果在第五層找不到可用的P,可用公式(2-4)、(3-1)等,將可用的P轉到第五層。 鏡射情形請自行想像。
公式2-4----F u' F' U' l' U l
2.5. 復原第三層的叉(Cr)
與(2-4)類似。
如果在第五層找不到可用的Cr,可用公式(2-5)、(3-1)等,將可用的Cr轉到第五層。 鏡射情形請自行想像
公式2-5----Ff u' F'f' U'u' l' Uu l
復原第四、五層
3.1. 復原第五層的叉(Cr)
本步驟的目標為轉成第五層中央3x3的小十字。
這個步驟只需要一個公式,而可能會有下圖中任一小圖的情況。如果不是下圖中任一小圖的情況時,只要稍微轉一下U或u層即可符合下列其中一情況。
公式3-1----R'r' U'u' F'f' Uu Ff Rr
3.2. 第五層的邊(Ed)的方向
本步驟的目標為轉成第五層5x5的十字。
這個步驟只需要一個公式,而可能會有下圖中任一小圖的情況。公式與(3-1)類似,只是視之為3階魔方I。
公式3-2----R' U' F' U F R
3.3. 第五層的角(Co)的位置
在本步驟中,先不要管第五層四個角的方向,以本文為例即不要管藍色那面是否在頂面,只要管四個角所屬的小方塊是否在正確的位置即可。
公式3-3----L R' U' R U L' U' R' U R 公式3-4----R' L U L' U' R U L U' L'
公式3-5----R' U' R U' R' U2 R U2 公式3-6----R U R' U R U2 R' U2
其它情況 可用公式(3-5)和(3-6)的組合來解。
公式3-7----(3-5)→U'→(3-6)→U 公式3-8----(3-6)→U→(3-5)→U'
其它情況 可用公式(3-7)和(3-8)的組合來解。
3.6. 復原第四、五層的翼(W)
優先將第五層的W轉好,然後再轉第四層的W(因為第五層有8個W,而第四層只有4個W)。
公式3-9----L R' u' R u L' u' R' u R 公式3-9----R' L u L' u' R u L u' L'
轉好第五層的W後,會遇到只剩第四層的2個W對調,如對調的兩個W在一個面上,則將該面放在左手做公式(3-9')→U'→(3-9')可以實現對調。如需要對調的兩個W在對角線上,做公式(3-9')→U'→(3-9'),則會出現兩個W在一個面的情況。
3.7. 復原第四層剩下的叉(Cr)
公式3-10----l R' F R F' l' F R' F' R 公式3-10----r' L F' L' F r F' L F L' 圖3
在使用本步驟的公式時,常要稍微暫時轉動一下各面,以配合公式中的位置,記得要把暫時轉動的過程記下來,以便轉好公式時再回復原狀。因為公式只能作3個Cr的調換,但如果最後只剩下2個Cr要對調的話,以圖3為例,可以借用U面的1個Cr當第3塊,作法為:b' R2→(3-10)→R2 b
3.8. 復原第四、五層剩下的點(P)
公式3-11----l R' u' R u l' u' R' u R 公式3-11----r' L u L' u' r u L u' L' 圖3-3
公式3-12----l R' d R d' l' d R' d' R 公式3-12----r' L d' L' d r d' L d L' 公式3-12----r u' r' u r' f r f'
公式3-12是四面式調換,這個公式並非必需,但公式轉法不難記。
,同上一步,在使用本步的公式時,經常要微微暫時轉動一下各面,以配合公式中的位置。因為公式只能作3個以上P的調換,但如果最後只剩下2個P要對調的話,以圖3-3為例,可以借用F面的1個P當第3塊,作法為:F'→(3-12)→F。
兩個點(P)的對調可用公式r U l' U' r' U l U',兩個叉(Cr)的對調可用公式M U l' U' M' U l U'。只要將點或叉放在F面和U面相同的位置。
與其他魔方聯繫
四階魔方,由於其中心塊不確定,所以還原到最後會出現特殊情況。而五階魔方,雖然表面上看是比四階“高了一階”,但其中心塊是固定的,也就使得其降階完成後並不會出現特殊情況,所以其解法也並不比四階複雜。

 五階魔方結構圖
五階魔方結構圖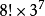


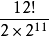




 五階魔方
五階魔方

