二進位制

二進位制是最簡單、最基礎的計數方式之一。生活中對二進制的掌握與運用，只須有一定的同異判別能力即可，對智力水平的要求比十進制低得多。不能因為電子產品廣泛套用二進制邏輯最簡單、最基本的特性而將它神秘化。

基本介紹

• 中文名：二進位制
• 簡稱：二進制

簡介

了解二進位制要先知道自然數，自然數及自然數記數法的一般定義出發，進行說明。自然數兩種基本定義：一稱為基數定義，表示個數；一稱為序數定義，表示順序關係。?

基數就是帶單位的數量，是相對直觀的概念，反映一種原始的抽象思維，記錄實物對象的重複量，離不開實物對象，只需數個數的水平，如結繩計數，尚不需形成整體意識，對心智比較也不需有過多的要求，就像兒童都有過認得一些零散的數（個數），但分不清大小的經歷一樣，在人類掌握排序概念以前，基數概念是最原始的數的概念。基數定義的自然數沒有排序功能，排序的概念則隸屬於自然數的序數定義。這是自然數的兩重天然屬性。一般認為，在19世紀下半葉之前，數學界對其中的區別並沒有清晰的認識。順序關係是自然數序數定義的核心。對序數的認識和運用是人類智力水平的又一次飛躍。基數是實物對象的簡單影射，序數則擺脫了實物對象的約束，需要比基數更進一大步的抽象能力和比較能力，並有自覺的全域觀念。任何用來表示順序的符號都是序數表示式，對使用者來說，都是自然數。如甲、乙、丙、丁，在生活中常用以表示順序，這時就屬於數的範疇，都是序數表示。甚至如座位三排五號也是序數，這種計數方法屬於自然數表示方式中的非位值進位制，它的位值用專用符號“排”和“號”來表示。可見，用來表示個數或序的符號都是自然數。

二進位制起源依據

根據符號的內部結構，自然數的表示法可分為非進位制、特殊位值進位制和位值進位制。非進位制是自然數的最原始的表示法，如簡單結繩計數形式。特殊位值進位制是指使用了進位的概念但藉助專用記號表示位值，沒有通用的位值概念。如上面提及的三排五號就是這種表示法，‘三’與‘五’是不同位上的值，這裡使用了進位的概念，並藉助專用符號‘排’來表示進位，而不是直接利用基本符號本身的位置關係來表示進位，因此稱為非位值進位制或特殊位值進位制。由於受專用進位符號的制約，這種表示法使用起來有明顯的局限性。古代的很多計數法如埃及、希臘、羅馬的計數法都屬於這類進位制。比如古希臘半島採用27個字母計數法，從1-9用九個字母表示，10-90 再用另外九個字母表示，100-900用剩下的九個字母表示，這種笨拙的特殊位值十進制計數法一直延續到文藝復興前夕。?

位值進位制是先進的表示法，顧名思義，直接利用基本符號本身的位置關係來表示進位，即“它用同樣的符號利用位置關係表示高位值”，因此稱為位值進位制。由於使用了位值的概念，位值進位制原則上可以把自然數推至無窮而不會出現邏輯困難。用十個基本符號來表示就稱為十進位制，用兩個基本符號來表示就稱為二進位制。

概念辨析?

由於所有數系的基礎都是對象的可數性或有序性即自然數，因此自然數記數法隨著數系的擴充，依次可以自然而然地成為整數、有理數、實數和複數的記數方式。對同一個數系來說，不同的記數方式是等價的，數系與記數方式之間不存在相互約束的關係。在討論周易與二進位制這個問題時，二進制算術是一個常出現的提法，但它是一種概念不清的錯誤提法，因為算術法則是來自數系自身的邏輯內涵的一種操作規定，只與數系自身有關，與記數法則毫無關係。採用同樣的記數法，只須對數系的定義進行一些簡單修改，它的算術就會面目全非。可見，在討論是否使用過二進制記數法這一問題的時候，把四則運算作為評判條件是錯誤的。

二進位制依據八卦原理

另外，有人以是否存在用二進制表示的小數作為二進制發明的判據，顯然也是錯誤的，因為記數法與數系之間不存在相互約束的關係，小數的發明遠在十進位制之後就是一個例子。值得一提的還有二進制的基本符號問題。二進制記數法的基本符號只需且只能有兩個基本符號，而這兩個符號可以是約定的任意字元，0和1僅僅是符合要求的任意符號組合中的一組而已，這也是很容易引起想當然的誤會。也許是因為我們對阿拉伯數字太熟悉了的緣故，常常會誤解只有寫成0和1形式的符號系列才是二進位制形式。其實，為了避免與十進制阿拉伯數字元號混在一起，現代運用中更多的是採用T(true)和F(false)或L(left)和R(right)作為基本符號。

條件

1．必須符合自然數定義，即必須是用來表示數量關係或順序關係的符號體系。?

2．基本的符號是只有兩個。

3．必須符合位值進位制的定義，即是否“用同樣的符號利用位置關係表示高位值”，而不是另外引入專用進位符號。以上三個條件是一個符號體系稱為二進位制體系的充分條件。

起源發展

從古到今的數學運算很大程度上是依靠了十進位制的偉大發明；而當今幾乎主宰了生產和生活的一切領域的計算機靠的是二進位制才形成了它的千變萬化。這兩種進位制的發明和確定，都和古代中國人的探索、創造有關。正整數逢十進一位，逢百進二位，逢千進三位，這種以十為基數的十進位制，看起來是十分簡單合理、自然而然的事情，但是人類還是經過艱辛探索才創造了這種進位制的。數字在中國出現，是在6000年前的新石器時代的晚期，那時用結繩、契木的方式計數。6000多年前的半坡遺址出土的陶片，上面已經出現了數字；距今4000年左右的陝西、山東、上海的出土文物中除表示個位的數字外，已經有10、20、30這樣的記號，表示當時已經使用十進位制。殷商時代的甲骨文上的13個計數文字中，除九個可以確定是個位數之外，還有四個就是十、百、千這樣的位值符號。甲骨文計數系統屬於十進位製成法分群數列，這種數系由1—9九個數字和若干個十進位制的位值符號組成。計數時先將兩組符號通過乘法結合起來以表示位值的若干倍，然後將分群後的位值符號組合（相加）起來。在出土的公元前13世紀的甲骨文中已經有“五百四十七天”的記載，《易經》中更有“萬有一千五百二十”這樣的記載。甲骨文的計數方式一直延續到現代。現代中國數字一二三四五六七八九，在唐代以前就已經形成，唐代還全面使用了大寫數字壹貳叄肆伍陸柒捌玖零，用在比較正規的場合，又叫做“官文書數字”。在確立了十進位制之後，古代中國還對數的概念進行了擴展，創造出了分數、小數、負數的概念，雖然分數線、小數點、負號不是中國的發明，但是對數的性質的認識，對數的概念的拓展，還是古代中國的天才創造。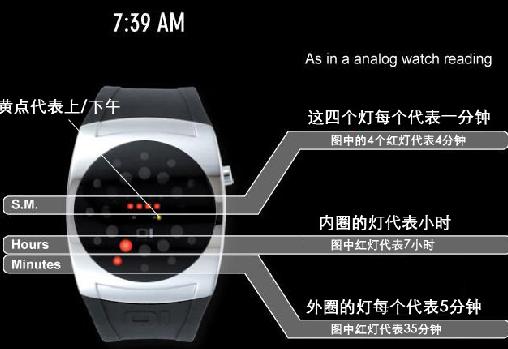

利用二進位制原理生產的手錶

演變歷史

中國數學史所討論的內容基本上都屬於算術範疇，在古代被稱為算學，即布算之學，重於計算技巧。而中國古代數學是專指邵雍為代表的研究傳統，即通過對抽象數的研究來探尋宇宙萬事萬物的內在邏輯。二進位制就是典型的代表，俗言中心中有數、定數就是這個數。伊川說：“數學至康節始入理也。”《四庫全書提要》評述道：“物生有象，象生有數，乘除推闡，務完造化之源者，是為數學。”就是說：主張物的產生必有象為先導，象的產生必有數為基礎，對數的關係進行深入探究，以達到窮盡造化演化規律的學問稱為數學。上海古籍出版社《四庫術數類叢書》出版說明指出：“(數學)實際是指據《周易》陰陽奇偶之數推衍出來的象數說。”

中國使用十進位制在世界最早。十進位制之所以在中國最早出現，和中國固有的文化是分不開的，漢字是方塊字而不是拼音文字，極大地促進了十進位制的形成。據史料記載，古代巴比倫人一直像後來的羅馬數碼那樣，用相加或累積計數，古埃及和古希臘也都是用特殊的記號來表示20、30、40等10的倍數，比如古希臘半島採用27個字母計數法，從1—9用九個字母表示，10—90再用另外九個字母表示，100—900用剩下的九個字母表示，這種笨拙的特殊位值十進制計數法一直延續到文藝復興前夕。印度人在公元6世紀才開始使用十進位制。而歐洲人正式採用十進位制的最早證據，是公元976年的一份西班牙文的抄本。十進位制是中國對人類作出的不可磨滅的重大貢獻。

二進位制是電子計算機的運算基礎，而二進位制的發明人是德國傑出數學家萊布尼（G.W.Leibniz,1646—1716），不過他發明二進位制是受了中國古代“先天八卦”的啟發。易經八卦相傳是伏羲畫卦，周文王重卦，太公作爻辭，是一雙魚太極圖，四周圍繞有乾坎震艮巽離坤兌八卦，這八卦就是由長短劃不同排列組合而成的符號。它的象徵意義是無極生太極，太極生兩儀，兩儀生四象，四象生八卦，八卦生六十四卦。每一卦都是由陽爻（—）和陰爻（- -）構成。如果以陽爻（—）為1，以陰爻（--）為0，按照二進位制的逢2進1的規則，則這從乾到坤的64卦均可以用0和1兩個數字表示出來。如第一卦乾卦為111111=63，第二卦為011111=62，第三卦為101111=61，這樣排列下去，第六十二卦為010000=2，第六十三卦為 100000=1，最後一卦為000000=0。統觀這從乾到坤的六十四卦的排列，其二進位制數序排列恰好為從63—0的自然數順序排列，真是天衣無縫，巧奪天工！當時，德國大數學家、微積分和數理邏輯的創始人萊布尼茨正在為創造一部乘法機而遇到困難，一籌莫展，正好他的朋友、到中國去傳教的教士白晉（J.Bouvet,1655—1730）從中國歸來，帶來了《六十四卦次序圖》和《六十四卦方點陣圖》，萊布尼茨如獲至寶，頓時感到陰陽兩個對立矛盾的面千變萬化的奇妙，對易經和八卦以及它最初的發明者伏羲充滿敬意，受到點撥和啟發，產生了他的二進位制的最早靈感。1703年萊布尼茨在《皇家科學院紀錄》雜誌發表了《二進位算術的解說——它只用0和1並論述其用途，以及伏羲氏所用的古代中國數學的意義》，論述了他的二進位制思想。他認為，“只有0和1的二進位制不但具有簡潔的形式，更可以表示宇宙間所有的量。所有的數通過1和0的方式表達，是何等美妙！”早在萊布尼茨之前，北宋的哲學家邵雍（1011—1077）就在他研究《易經》的著作中提出了比較完備的二進位制思想,可惜他的二進位制思想沒有傳播開來。

原理剖析

自然數的概念在數學上一直被當做最明顯，最基本的概念來套用，直到上世紀末，在數學的公理化方法發展的影響下，才提出“自然數是什麼”的問題。基於自然數的兩種功能層次，即表達個數的概念和表達順序的概念，19世紀末出現了著名的康托爾基數公理和皮亞諾序數公理，從數學邏輯的角度對什麼是個數和什麼是順序號作出定義。?

個數和順序都是顯而易見的概念。但從文明發展的角度來說，異同概念的出現是理性的起點，個數概念的出現是一個巨大進步，順序概念的出現又是一個巨大的進步。對個數（基數）和順序（序數）作出規範定義將大大方便文明史的研究，也有助於抽象數學本身的發展。?

基數就是個數，是最原始的、很直觀的數的概念，判斷掌握基數概念的標準是只需有一一對應地數個數能力，尚不要求形成整體意識，也不要求有一般的比較概念。自然數的基數理論，即康托爾基數公理，是以集合和一一對應的概念為基礎來定義的。由於在定義中不能隱含順序概念在裡面，使用集合的概念來定義是非常巧妙的，但也相當拗口。?

給定兩個集合A、B，如果存在一個規則f，對A中的每一個元素a，在B中唯一確定b（即a在f下的像），而B中任一元素b均由A中某一相應元素a唯一確定，那么就說f是A到B的一個一一對應。存在一一對應的兩個集合稱為等價的，取定一個集合A，把所有與A等價的集合放在一起，作成一個集合的類W，W中所有集合所共有的屬性稱為A的基數，簡言之，類W本身就稱為A的基數。集合的基數實際上就是集合中元素的個數。自然數的序數理論是利用兩個的基本概念第一個與下一個以及四個公理來定義的。第一個通常可以記為1，不過不如記為n0更有普遍意義。所謂自然數（序數），是指滿足以下性質的集合N中的元素：n0是N的一個元，它不是N中任何元的後繼者，若n的後繼者用n+來表示，則對於N中的任意元n, n+不等於n0。（註：n0是指定的順序起點而不作證明）。對於N中任意元n, 存在而且僅存在一個後繼者n+。對N中任何兩個元n和m, 若n+=m+，則n=m.4）N的一個子集M，若具有以下xi性質： n0屬於M；對於任意m屬於M，必有m+也屬於M；則M=N。