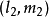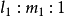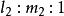基本介紹
- 中文名:二次錐面
- 外文名:quadric conical surface
- 類型:橢圓、雙曲、拋物錐面
- 定義:方程時二次的錐面
- 一級學科:數學
- 二級學科:空間解析幾何
曲面介紹,截平面,二直線夾角,
曲面介紹
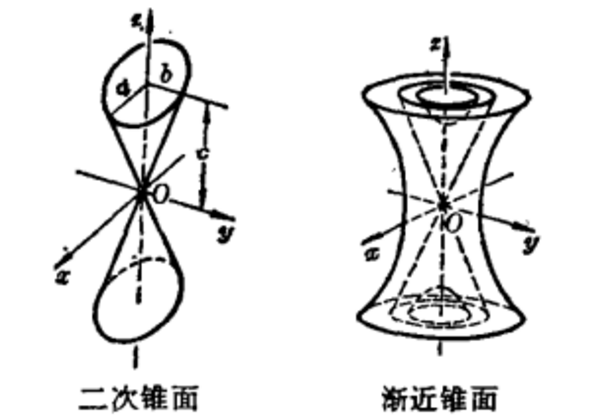
二次錐面(quadric conical surface)亦稱“橢圓錐面”,錐面的一種。空間直角坐標系中由方程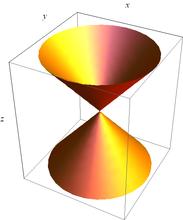


截平面
平面
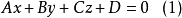
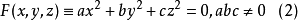
定理1,平面(2)與二次錐面(1)相切的充要條件是

定理2,平面(1)截二次錐面(2)於一條無心曲線的充要條件是
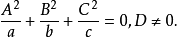
定理3,平面(1)截二次錐面(2)於一條有心曲線的充要條件是

定理2和定理3是定理1的直接推論。
定理4,一平面截二次錐面(2)於一條有心曲線,該曲線中心為 ,M非原點,則該截平面的方程是
,M非原點,則該截平面的方程是

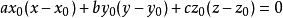
定理5,設點 滿足
滿足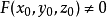 ,並且二次錐面(2)過點M的切線存在,則以點M為頂點的二次錐面(2)的切線軌跡,即切錐面的方程時
,並且二次錐面(2)過點M的切線存在,則以點M為頂點的二次錐面(2)的切線軌跡,即切錐面的方程時

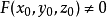

二直線夾角
二次錐面(2)上兩條直母線必在其頂點處相交,它們確定一個通過原點的平面 ,故二次錐面(2)上兩條直線總可以用方程
,故二次錐面(2)上兩條直線總可以用方程

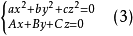
設方程(3)表示的直線的方向數是X:Y:Z,則



由方程(4)求得二解 和
和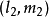 ,則二直線的方向數是
,則二直線的方向數是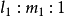 和
和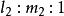 ,從而可求得由方程(3)表示二直線的夾角。
,從而可求得由方程(3)表示二直線的夾角。