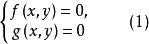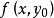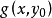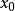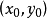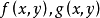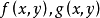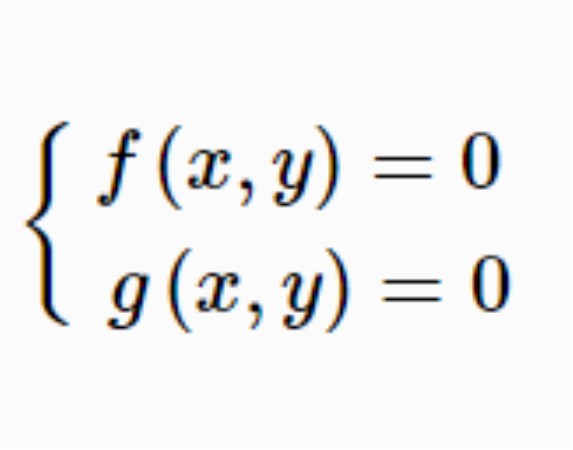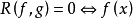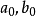二元高次方程組(system of binary equations of higher degree)是一種代數方程組,若兩個代數方程f(x,y)=0,g(x,y)=0組成的方程組中的f(x,y),g(x,y)是復係數二元多項式,其中至少有一個為高次的,則稱次方程組為二元高次方程組。
基本介紹
- 中文名:二元高次方程組
- 外文名:system of binary equations of higher degree
- 所屬學科:數學
- 所屬問題:高等代數(多項式)
- 簡介:一種代數方程組
基本介紹,二元高次方程組的解法,相關定理,
基本介紹
若代數方程組
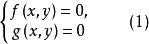
二元高次方程組的解法
解方程組(1)的一般方法是把f(x,y)與g(x,y)看成x的多項式,設
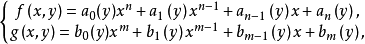
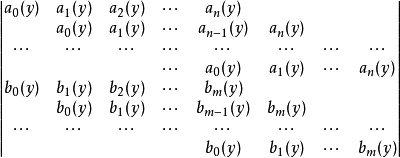
相關定理
引理 設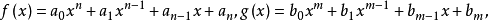 ,是數域P上的兩個非零多項式,
,是數域P上的兩個非零多項式,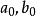 不全為零,則
不全為零,則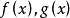 在
在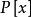 中有非常數的公因式
中有非常數的公因式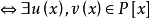 ,使得
,使得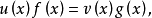 這裡
這裡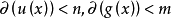 。
。
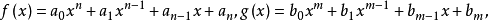
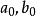
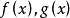
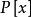
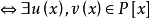
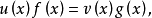
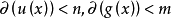
定理2 若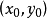 是
是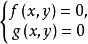 的一個複數解,則y0是Rx(f,g)的一個根,反之,若y0是Rx(f,g)的一個復根,那么
的一個複數解,則y0是Rx(f,g)的一個根,反之,若y0是Rx(f,g)的一個復根,那么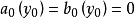 ,或者存在一個複數
,或者存在一個複數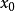 使
使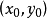 是上方程組的一個解。
是上方程組的一個解。
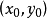
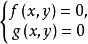
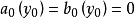
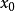
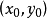
欲求二元高次方程組: