乘法電路(multiplying circuit)是一種完成兩個互不相關的模擬信號相乘作用的電子器件。它可以將兩個二進制數相乘。它是由更基本的加法電路組成的。
基本介紹
- 中文名:乘法電路
- 外文名:multiplying circuit
- 學科:計算機科學與技術
- 類別:運算電路
- 分類:並行、串列等
- 主要套用:信號處理
基本概念
乘法器



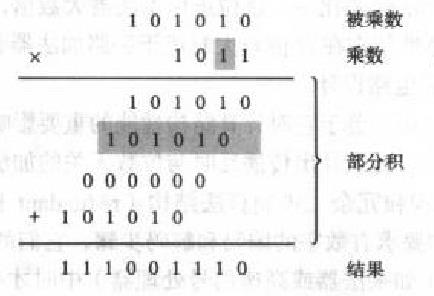
乘運算

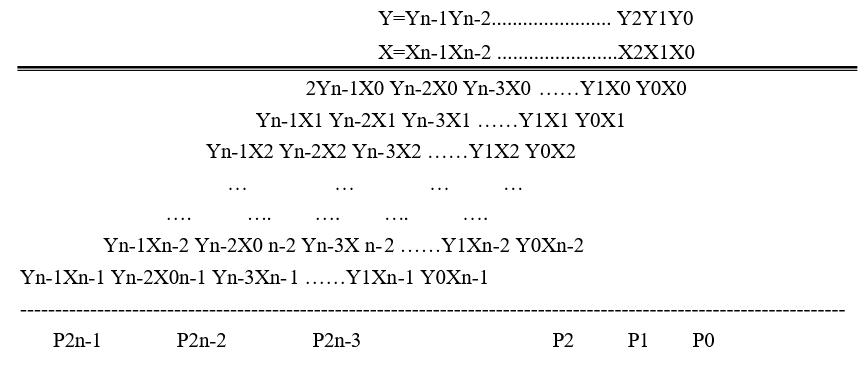

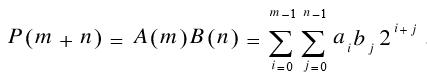
乘法器類型
串/並行乘法器
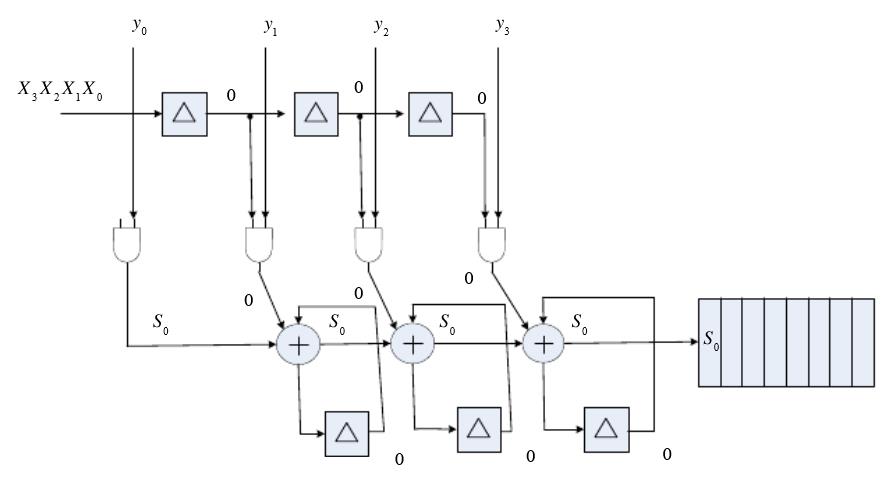
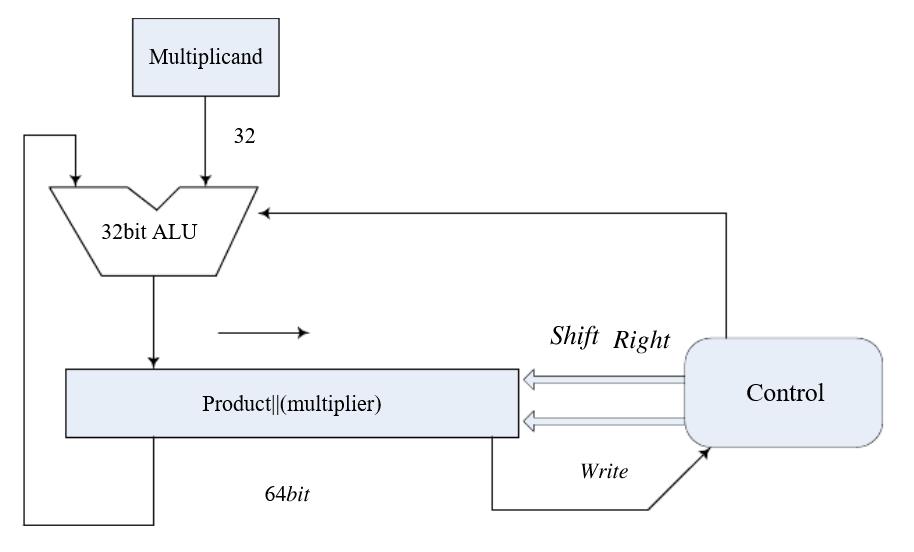
位移和添加乘法器
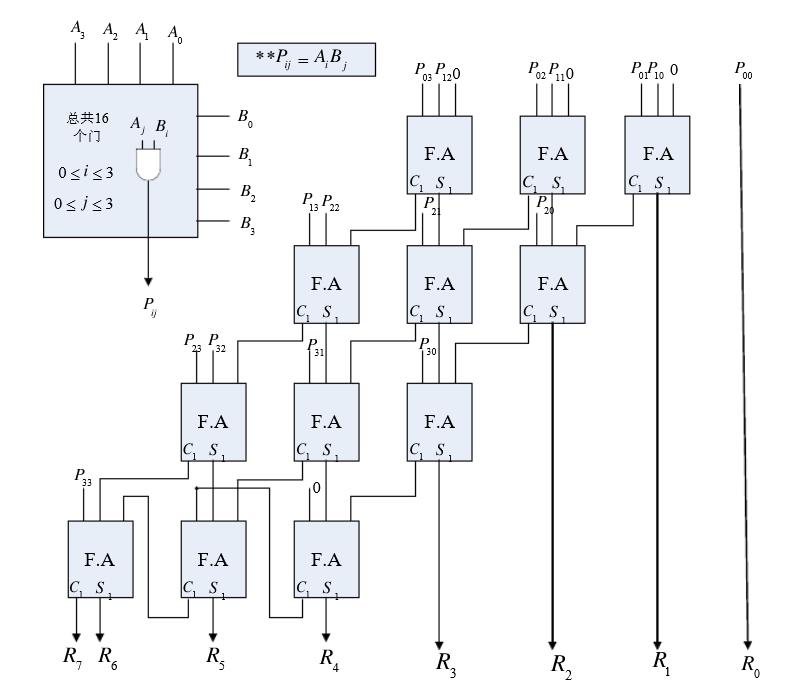
陣列乘法器

乘法電路(multiplying circuit)是一種完成兩個互不相關的模擬信號相乘作用的電子器件。它可以將兩個二進制數相乘。它是由更基本的加法電路組成的。







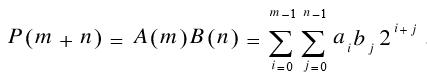



乘法器可以用更普遍的方式來表示。每個輸入,局部乘積數,以及結果都被賦予了一個邏輯名稱(如A1、A2、B1、B2),而這些名稱在電路原理圖中就作為了信號名稱。在原理圖的乘法例子中比較信號名稱,就可以找到乘法電路的行為特性。在乘法器...
兩個輸入信號均為雙極性的模擬乘法器。它是在信號檢測和控制電路中套用較多的一個單元。定義 兩個輸入信號均為雙極性的模擬乘法器。它是在信號檢測和控制電路中套用較多的一個單元。電路圖 電路圖如圖1(a)所示。忽略基極電流後,其...
模擬乘法器是對兩個模擬信號(電壓或電流)實現相乘功能的的有源非線性器件。概念 主要功能是實現兩個互不相關信號相乘,即輸出信號與兩輸入信號相乘積成正比。它有兩個輸入連線埠,即X和Y輸入連線埠。模擬乘法器是輸出電壓與兩路輸入電壓之...
模擬相乘器是完成兩個模擬信號瞬時值相乘功能的電路或器件。其主要技術指標是工作象限、線性度和饋通度。它利用電晶體的基-發射結電壓與集電極電流的非線性特性實現相乘。模擬相乘器在諸如乘、除、開方、平方等模擬運算方面和混頻、調製、...
乘法電路中的編碼邏輯會引入‘’異或‘’運算,這部分邏輯會干擾HAG的提取,因此應該對這部分邏輯進行預處理。HAG提取算法 提取HAG是以AIG為基礎,構建AIG的偽代碼如下。Algorithm create vetex(p₁,p₂){Special case preprocess;If...
以乘法電路為例:設計思路如上,具體電路如下(未加入溫度補償電路)利用二極體的PN結,可以實現對數運算。但是在實際套用的過程中,常把電晶體的基極與集電極短路,接成二極體的形式以增加集電極電流動態運用範圍。輸出電壓幅度不能超過0.7V...
布爾乘法和與門電路 根據布爾代數,與門是一個乘法器。這與常規的十進制乘法運算相同,因為0乘以1等於0,1乘以1等於1,正如與門真值所示。布爾乘法等價於一個與門電路,其基本法則用與門表示如下:與門的布爾表達式 (1)2輸人與門...
七.模擬信號運算電路 理想運放的特點(虛短虛地);比例運放(反向比例運放,同向比例運放,差分比例運放);求和電路(反向輸入求和,同向輸入求和)積分電路,微分電路;對數電路,指數電路;乘法電路,除法電路。八.信號處理電路 有源濾波...
第5章算術邏輯運算電路 5.1基本算術運算電路’5.1.1加法器 5.1.2數值比較器 5.1.3移位運算 5.2複雜運算電路的設計 5.2.1用基本運算電路配合控制程式的實現方法 5.2.2乘法電路 5.2.3除法電路 5.3BCD碼算法 5.3.11位...
邏輯設計)12.6加法器的動作和設計 12.6.1半加器 12.6.2全加器 12.6.3設計4位加法器 12.7乘法器的動作和設計 12.7.14位X4位乘法器電路 12.7.2.用HDL描述的乘法電路 12.7.3由HDL組成的設計是萬能的嗎 ...
9.3.2電晶體可變跨導型乘法電路 9.4單片集成模擬乘法器 9.5乘法器的參數 9.6模擬乘法器在模擬運算中的套用 9.6.1除法運算 9.6.2平方和平方根運算 9.6.3均方根運算 9.6.4函式發生電路 9.7模擬乘法器在通信電路中的套用...
最典型的模擬電路套用包括:放大電路、振盪電路、線性運算電路(加法、減法、乘法、除法、微分和積分電路)。運算連續性電信號。數字電路 數字電路又名邏輯電路,是一種將連續性的電信號,轉換為不連續性定量電信號,並運算不連續性定量...
門電路幾乎可以組成數字電路裡面任何一種複雜的功能電路,包括類似於加法、乘法的運算電路,或者暫存器等具有存儲功能的電路,以及各種自由的控制邏輯電路,都是由基本的門電路組合而成的。電路結構類型 門電路輸出端的電路結構有三種型式:有...
5.10.1 阻抗模擬變換器的電路結構及其工作原理 5.10.2 模擬對地電感電路 5.10.3 模擬對地電容電路 5.10.4 模擬對地負阻抗電路 5.11 模擬電感器 5.12 電容倍增器 本章小結 思考題與習題5 第6章 模擬乘法器電路 6.1 模擬...
乘法(Multiplication)是由被稱作乘法器的數字電路來完成的。在同一時間,數總是被2乘.因此需要兩個輸入。乘法器的輸出是積。乘法器的乘法運算主要是通過移位和加法電路來實現的。被乘數(二進制數)不斷地向左移位來實現連續乘2,變成積...
MLT04的輸入失調電壓的誤差可以採用可變失調電壓調整電路來消除。這種電路還可以減小乘法器核心中的輸出偏置電壓、增益誤差以及非線性器件引起的固有誤差。乘法器的內部非線性是器件的固有誤差。它指的是所有成對輸入值的實際輸出與理想的線性...
減法電路是基本集成運放電路的一種,算術運算電路主要包括數字加法器電路、數字減法器電路、數字乘法器電路和數字除法器電路。由於基本的算術運算加法、減法、乘法、除法最終都可歸結為加法或減法運算,因此,在算術運算電路中數字加法器電路與...
例3.3 用隔級正負邏輯符號變換法分析組合邏輯電路 例3.4 組合電路用其他邏輯門實現 例3.5 多數表決電路設計 例3.6 邏輯運算、算術運算電路設計 例3.7 碼制變換電路的設計 例3.8 乘法電路設計 例3.9 8-3線優先編碼器CT1148...
5.3.2 利用對數和指數電路的乘法電路 5.3.3 變跨導式模擬乘法電路 5.3.4 模擬乘法器的套用 5.3.5 除法運算電路 5.4 有源濾波電路 5.4.1 濾波電路的功能、分類和主要參數 5.4.2 有源濾波電路的分析方法 5.4.3 有源...
7.2 運算電路 158 7.2.1 比例運算電路 158 7.2.2 求和電路 161 7.2.3 積分電路和微分電路 163 7.2.4 對數和指數運算電路 166 7.2.5 乘法運算電路 167 7.3 有源濾波電路 169 7.3.1 低通濾波電路 171 7.3.2 高通...
6.2 基本運算電路 113 6.2.1 比例運算 113 6.2.2 加法運算 115 6.2.3 減法運算 116 6.2.4 微積分運算 118 *6.2.5 乘法運算電路 119 思考題 121 *6.3 有源濾波和精密整流電路 121 6.3.1 有源濾波電路 121 6.3...
