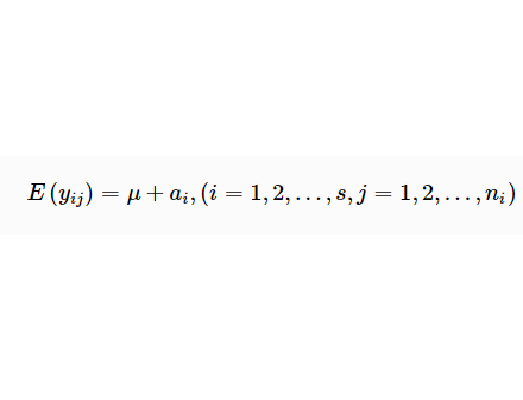基本介紹
在有一個或幾個因子(自變數)的多水平的實驗中,描述一個因子在各水平上對反應量(因變數)影響大小的度量。對有S個水平的單因子A的試驗,若隨機變數
是在第
次試驗中於第
個水平上的觀測值,則模型為
這裡E是期望,
是總平均,
即A因子第
個水平的
主效應。應當注意的是,由於它在平均意義上進行估算,所以即使一個主效應的值比較小,也不表明該因子不重要;同時,在互動作用顯著的情況下,對主效應的直觀解釋可能會發生誤解。在有的實驗研究中,主效應並不一定比互動作用更為重要。在實驗設計中,只有主效應而不考慮互動效應的模型,稱為
可加性模型,這在區組設計中常常使用。
主效應與互動作用
因素的主效應和因素之間的
互動作用是析因試驗設計中的兩個基本概念。考慮兩個2水平因素的析因試驗,設因素A的兩個水平為
和
,因素B的兩個水平為
,它們的所有可能的水平組合為
,如表1(0)所示,稱其為2
2析因試驗。這裡約定,
既代表因素水平組合或處理,又表示在這種因素水平組合或處理下的指標真值或回響值。因素主效應反映因素對指標的影響大小,常用其回響值的改變數來表示。在2
2析因試驗中,對於因素A,當因素B取B
1時,A從A
1變為A
2所引起的回響值的變化為
;當因素B取B
2時,A從A
1變為A
2所引起的回響值的變化為
。這兩個回響值的改變數稱為4的兩個
簡單效應。
因素的簡單效應描述了其它因素固定情況下這個因素對指標的影響大小。因素A的
主效應自然應定義為A的兩個簡單效應的平均值。它也可表示為A取A
1時回響的平均值
與A取A
2時回響的平均值
之差。因素A的
主效應常用同一大寫字母4表示,於是
類似可定義因素B的主效應為
表1(I)、(Ⅱ)是兩個2
2析因試驗的數字例子。由上述定義可知,對於(I),
因素間的互動作用是指因素之間的一種搭配作用。在2
2析因試驗中,如果因素A在兩個水平上的回響值的改變數,不管因素B的水平如何都是一樣的,即A對指標的影響與B取什麼水平無關,那么我們就說因素A與B之間
沒有互動作用或A與B之間的互動作用為零,如果因素A在兩個水平上的回響值的改變數隨著因素B的水平不同而不一樣,即A對指標的影響取決於B取什麼水平,那么我們就說因素A與B之間
存在互動作用,其大小通常用因素B取B
2時A從A
1變為A
2所引起的回響值的改變數
減去因素B取B
1時A從A
1變為A
2所引起的回響值的改變數再除以2來表示。因素A與B的
互動作用記為A×B,或簡記為AB。於是
即它也等於A與B都取第1水平和第2水平時的回響值的和與A或B只取第1水平或第2水平時的回響值的和之差的一半。按此定義,對於表1中的(I),有A×B=0,對於表1中的(Ⅱ),有A×B=-29,這說明表1(I)中的兩個因素沒有互動作用,而表1(Ⅱ)中的兩個因素有互動作用。它們可分別畫出如圖1(a)、(b)所示的圖形。從圖上看出,沒有互動作用畫出的兩條直線是平行的,有互動作用畫出的兩條直線是相交的。
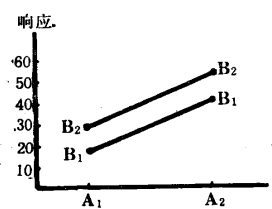 圖1(a)
圖1(a)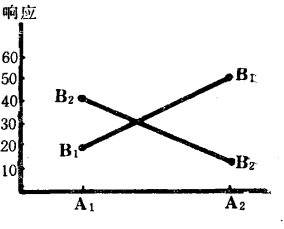 圖1(b)
圖1(b)主效應和互動作用統稱為析因效應或簡稱效應。在分析時它們需要同時加以考慮。當因素之間的互動作用很小時,各個因素對指標的影響可以看作是相互獨立的,一個因素對指標影響的大小用該因素的主效應表示。當因素之間的互動作用很大時,各個因素的主效應意義就不大了。例如,在表1(Ⅱ)的例中,前已算出因素A的主效應A=1,相對說來是比較小的,但我們不能輕易就說因素A對指標的影響不大。因為因素A與B的互動作甩A×B=-29,其絕對值相當大。這表明因素A對指標有影響,只是這種影響與因素B的水平有關。互動作用提供的信息有時比主效應的更有用。大的互動作用往往掩蓋住了主效應的真實情況。表1(Ⅱ)的例子說明了這點。在互動作用比較大的場合,要對一個因素作出推斷,試驗者必須考察這個因素的各個水平與另一個因素的各個水平的種種搭配情況下的表現,加以比較後再作結論。
多因素析因試驗較之傳統的每次試驗一個因素的多因素試驗方法有著明顯的優點。首先,多因素析因試驗不僅能考察各因素的主效應,還能分析因素之間的互動作用。它不象每次一個因素的試驗只能考察各個因素的單獨影響,因而析因試驗所得結論一般說來比每次一個因素的試驗更符合實際。例如,在一項兩個2水平因素的試驗中,假如每次一個因素的試驗顯示出A1B2比A1B1好,A2B1比A1B1好, 那么一個自然的推論應是A2B2會更好。然而,當因素之間存在互動作用時,這個結論可能是完全錯誤的。表1(Ⅱ)的數字例子就屬於這種情況。其次,由於析因試驗的全部觀測值能一起用來分析各個因素對指標的影響,而每次一個因素的試驗只能用一個因素的試驗結果單獨分析這個因素的作用,所以要達到同樣的分析精度,每次一個因素的試驗所需要的試驗次數一般比析因試驗的多,即析因試驗更有效。例如,在一項兩個2水平因素試驗中,每次一個因素進行試驗,因素A的一個簡單效應為A2B1-A1B1,因素B的一個簡單效應為A1B2 -A1B1。因為試驗存在誤差,為了能用觀測到的簡單效應的平均值估計兩個因素的效應,每種處理必須進行(比如說)兩次試驗。這時共需作6次試驗。但若施行析因試驗,則只需增加一個試驗A2B2,即可求得因素A的兩個效應A2B1-A1B1,A2B2-A1B2的估計以及B的兩個簡單效應A1B2-A1B1,A2B2-A2B1的估計,分別加以平均就可求得A與B的主效應的估計。可以證明,這樣兩種試驗的精度是一致的。但這時的析因試驗只要作4次試驗。再者,由於析因試驗考察一個因素時是在其它因素的不同水平上進行的,因而所得結論能用於比較廣泛的試驗條件。析因試驗的主要缺點是,當考察的因素比較多時,所需要的試驗次數太多。例如,10個2水平因素的析因試驗的所有可能的水平組合有210=1024,7個3水平因素的析因試驗的所有可能的水平組合有37=2181等。與此有關的是試驗太多就很難保持試驗環境的一致。為了克服析因試驗的這些困難,統計學家已成功地研究出了一套諸如部分析因試驗、混雜法和強調效率的多因素試驗方法。
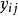



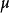
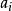

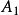



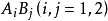

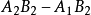
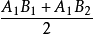


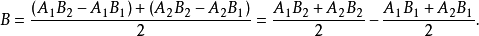


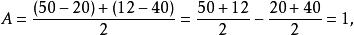
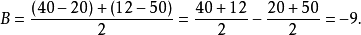


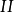


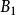


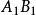




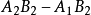
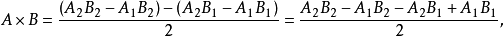
 圖1(a)
圖1(a) 圖1(b)
圖1(b)