不規則匹配法是一種標準數獨技巧，是一種異數鏈結構，而使用多個數、跨區進行討論，得到刪數結論。
基本介紹
- 中文名：不規則匹配法
- 外文名：Irregular Wing
- 別名：異數短鏈
技巧簡介,技巧使用,首尾數對匹配法（W-Wing）,隔一數對匹配法（M-Wing）,分裂匹配法（Split-Wing）,拐角匹配法（Local-Wing）,雜合匹配法（Hybrid-Wing）,技巧名稱,
技巧簡介
不規則匹配法是一種特殊的異數鏈結構。最初的這些構型，都是使用分類討論思想，找共同對應的刪數。可以認為，不規則匹配法就是一種異數短鏈結構。而一般來說，不規則匹配法長度均為5。它含有多種類型：首尾數對匹配法（W-Wing）、隔一數對匹配法（M-Wing）、分裂匹配法（Split-Wing，簡稱S-Wing）、拐角匹配法（Local-Wing，簡稱L-Wing）、雜合匹配法（Hybrid-Wing，簡稱H-Wing）。
閱讀本節內容請先學會鏈的相關知識。
不規則匹配法在Sudoku Explainer是沒有難度係數分配數值的。經過更新之後，難度係數分配如下：
| 技巧名 | 英文名 | 難度係數 |
|---|---|---|
首尾數對匹配法 | W-Wing | 4.4 |
隔一數對匹配法 | M-Wing | 4.4 |
分裂匹配法 | Split-Wing、S-Wing | 4.5 |
拐角匹配法 | Local-Wing、L-Wing | 4.5 |
雜合匹配法 | Hybrid-Wing、H-Wing | 4.5 |
技巧使用
首尾數對匹配法（W-Wing）
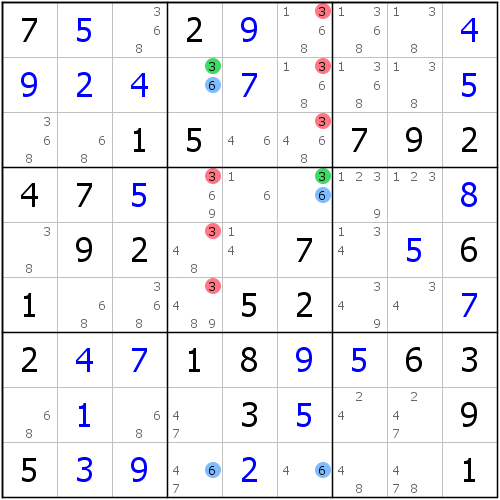
我們把r5c9(7)作為鏈頭的話，則它會和在同一單元格內的候選數4構成強關係，然後r5c9(4)會和r5c7(4)構成弱關係，r5c7(4)會和r7c7(4)呈強關係，r7c7(4)會和r7c8(4)呈弱關係，r7c8(4)會和與同一單元格內的候選數7構成強關係。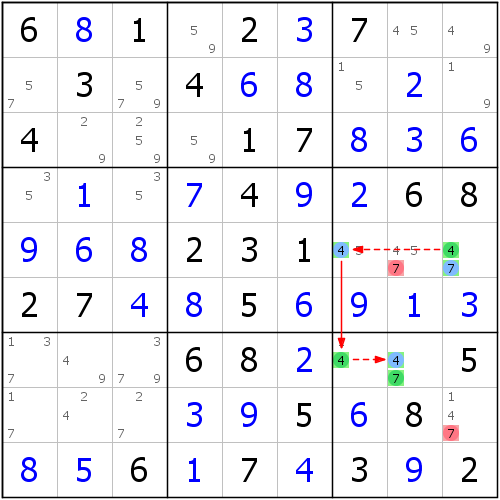
W-Wing
W-Wing寫成鏈後便成了這樣：
r5c9(7=4)-r5c7(4)=r7c7(4)-r7c8(4=7) => r5c8, r8c9<>7
同一格的不同候選數之間的強弱關係可以直接寫在同一對括弧內。
隔一數對匹配法（M-Wing）
鏈如下所示：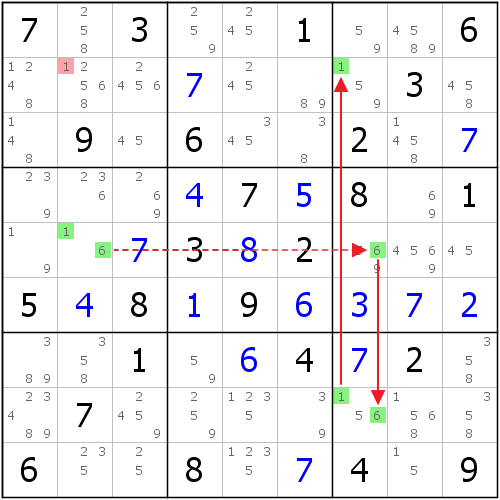
M-Wing
M-WingE2(1=6)-E7(6)=H7(6-1)=B7(1) => B2<>1
我們可以看到這條鏈很簡單，當E2<>1的時候，會得到B7=1。
抽象出結構，我們會發現，有兩個“16”，並且它們之間隔了一個候選數作為它們的橋樑。所以它被稱為隔一數對匹配法。
分裂匹配法（Split-Wing）
鏈如下表示：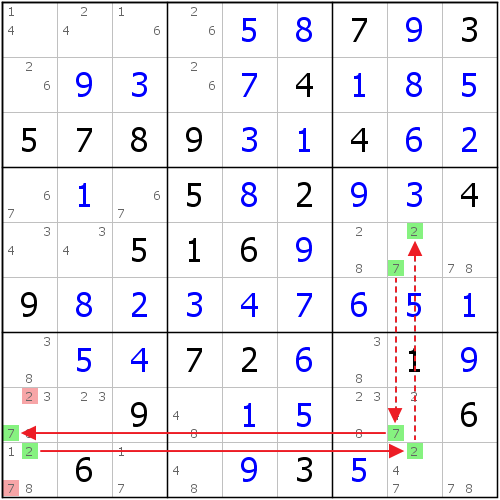
S-Wing
S-WingI1(2)=I8(2)-E8(2=7)-H8(7)=H1(7) => H1<>2, I1<>7
拐角匹配法（Local-Wing）
鏈如下表示：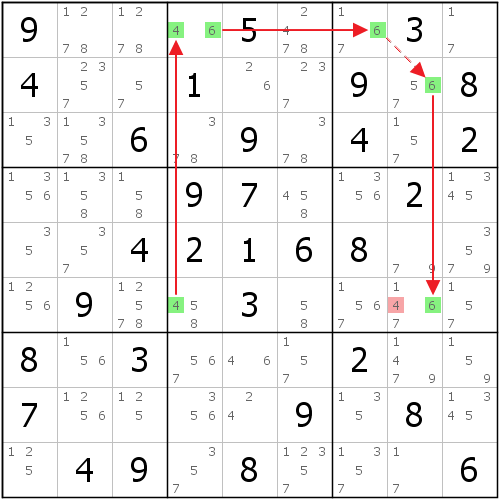
L-Wing
L-WingF4(4)=A4(4-6)=A7(6)-B8(6)=F8(6) => F8<>4
雜合匹配法（Hybrid-Wing）
鏈如下表示：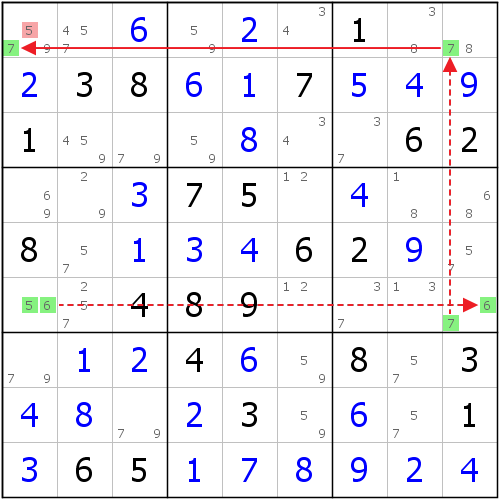
H-Wing
H-WingF1(5=6)-F9(6=7)-A9(7)=A1(7) => A1<>5
技巧名稱
由於本節內容的名稱比較容易混淆，故此處僅列舉出各種技巧的標準類型的AIC的寫法，括弧表示在一個單元格內的強關係或弱關係。如果您想得到其他變形結構對應的AIC的話，您可以嘗試去枚舉其結構。
名稱 | AIC寫法 | 刪數方式 |
XY/Y-Wing | (x=y)-(y=z)-(z=x) | 鏈頭鏈尾共同對應 |
XYZ-Wing | (x=y)-(y=xz)-(z=x) | 鏈頭鏈尾共同對應 |
M-Wing | (x=y)-y=(y-x)=x | 鏈頭鏈尾共同對應 |
W-Wing | (x=y)-y=y-(y=x) | 鏈頭鏈尾共同對應 |
S-Wing | x=y-(y=x)-x=y | 鏈頭（x格）的y，鏈尾（y格）的x |
H-Wing | (x=y)-y=(y-z)=z | 鏈尾（z格）的x |
(x=y)-(y=z)-z=z | 鏈尾（z格）的x | |
L-Wing | x=(x-z)=(z-y)=y | 鏈頭（x格）的y，鏈尾（y格）的x |
