分支匹配法

分支匹配法是一種標準數獨技巧，使用多個數、跨區進行討論，得到刪數結論。

基本介紹

• 中文名：分支匹配法
• 外文名：Regular Wing
• 別名：規則匹配法、規則形態法

技巧簡介

在標準數獨技巧體系之中，有一類技巧，英文翻譯為“Wing”。而這類技巧因為形狀變化多端，故一直沒有給出翻譯名稱。在《數獨了不起：全世界最流行的填字遊戲背後的數學》中，X-Wing（二鏈列、四角對角線法則）被翻譯為“X形態法”。

Wing類型技巧分為三個大類，第一類是規則Wing類技巧，稱為“規則匹配法”（或“分支匹配法”）；第二類是不規則Wing類技巧，稱為“不規則匹配法”；第三類是同數異化結構，一共有兩個：X-Wing（二鏈列）和Broken-Wing（守護者）。本節展示第一類Wing技巧。

規則匹配法（分支匹配法）在Sudoku Explainer之中的難度係數分配如下：

技巧名	英文名	難度係數
雙分支匹配法	XY-Wing、Y-Wing	4.2
三分支匹配法	XYZ-Wing	4.4
四分支匹配法	WXYZ-Wing	4.6

技巧使用

雙分支匹配法（XY-Wing/Y-Wing）

如圖所示，我們觀察到，r1c2的候選數為{38}，r2c3的候選數為{48}，而在r5c2，候選數為{34}。我們可以做出一系列的推理：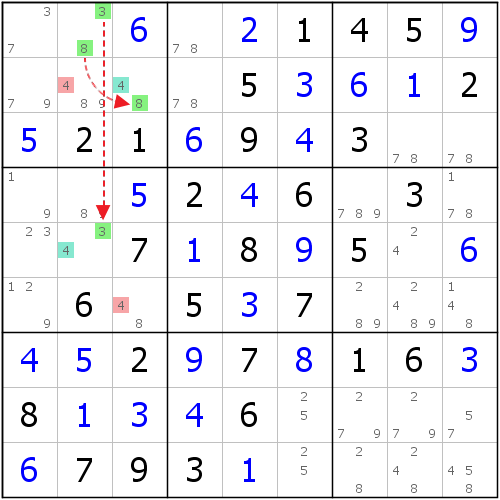

雙分支匹配法

（1）如果r1c2=3，則r5c2<>3，只得填4；

（2）如果r1c2=8，則r2c3<>8，只得填4。

這個時候，我們發現，不管怎么樣，要么r5c2=4，要么r2c3=4，反正始終這2格內必有一格要填入4。也因此，它們兩格共同對應的單元格將不得填入4。它們共同的單元格是r2c2和r6c3，所以r2c2, r6c3<>4。

這被稱為分支匹配法。由於只涉及兩種不同情況，所以也被稱為雙分支匹配法。而其中的r1c2單元格，被稱為折點（Pivot Cell）。

當做題的時候，發現有3格可以滿足候選數為{ab}、{bc}、{ac}，並且有兩組單元格同時在一個單元內的時候，我們就可以採用這個技巧進行刪數了。

三分支匹配法（XYZ-Wing）

如圖所示，發現在r3c1的候選數是{19}，r3c2的候選數是{149}，r7c2的候選數是{14}。按照剛才的雙分支分支匹配法的推理方式進行推理，此時將會具有3種不同的情況：

三分支匹配法

（1）r3c2=1；

（2）r3c2=4，則r7c2<>4，則r7c2=1；

（3）r3c2=9，則r3c1<>9，則r3c1=1。

這時我們發現，不管怎么樣，始終都將有一個格子（r3c2、r7c2或者r3c1）會填入1。剛好，這3格都可以對應到單元格r1c2上，所以r1c2<>1。

這就是三分支匹配法。就只是在雙分支上多了一個沒有太大影響的假設情況而已。但是僅僅是這一點，讓我們的觀察就加大了不小的難度。

四分支匹配法（WXYZ-Wing）

如圖所示，此時我們發現同樣具有如下的結構：A8={2456}，A9={25}，F8={45}，G8={56}。此時進行假設：

四分支匹配法

（1）A8=2，則A9<>2，則A9=5；

（2）A8=4，則F8<>4，則F8=5；

（3）A8=5；

（4）A8=6，則G8<>6，則G8=5。

無論怎么填，這4格里始終有一個格子填5，剛好，這4格都可以對應到單元格B8上，所以B8<>5。

特殊用法

偽數組觀察方式

如四分支匹配法示例。偽數組的思路是：按照是否是跨區數組討論填數情況。最終發現，能夠重複的僅含有候選5。因此刪除所有5的交集。

只要能夠使用偽數組的方式觀察的，都可以稱為分支匹配法。

鏈觀察方式

所有的分支匹配法都能夠改成超鏈寫法。比如所有分支匹配法，將可以抽象成結構(x=y)-y=x。“y=x”產生於強待定數組區域內。所以規則匹配法又被稱為“1 Cell + n”邏輯，直譯為“一格帶n數”邏輯。

飽和分支匹配法

如圖所示。有一部分的分支匹配法不能改寫成上述寫法，但一樣屬於分支匹配法。例如此示例。此處不對其進行邏輯的講解。

多分支匹配法

技巧名稱由來

在標準數獨的系統命名法中，規則匹配法的命名是看結構記憶體在有多少種不同的數字。除了雙分支匹配法以外，每多一個數，就加一個字母。從XY開始。比如三分支匹配法就是XYZ-Wing，而四分支匹配法已經無法往後加字母，就在其前面加入字母W，即WXYZ-Wing。五分支匹配法就是VWXYZ-Wing。

這種技巧最多能夠達到9個分支（使用跨區數組證明），即英文名為RSTUVWXYZ-Wing。

而需要注意的是，由於分支匹配法均可以看成跨區顯性數組，故分支數大於5的，都能採用跨區隱性數組互補理解，故多於4個分支的結構，一般只存在於理論之中。