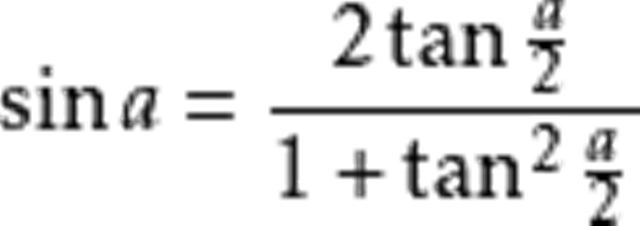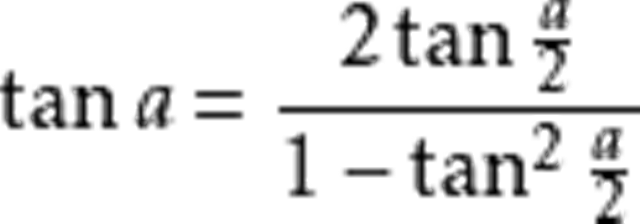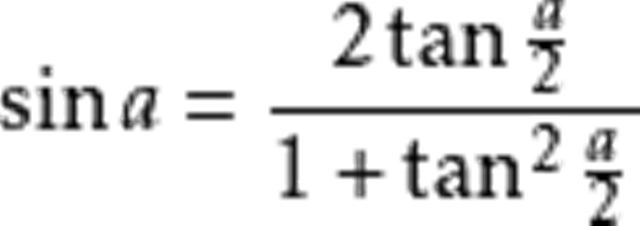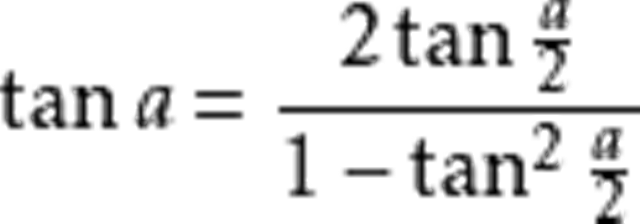基礎三角恆等式
sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
sinα/cosα=tanα
secα/cscα=tanα
cosα/sinα=cotα
兩角和與差
倍角公式
二倍角
sin2α = 2cosαsinα
= sin2(α+π/4)-cos2(α+π/4)
= 2sin2(a+π/4)-1
= 1-2cos2(α+π/4)
cos2α = cos2α-sin2α
= 1-2sin2α
= 2cos2α-1
= 2sin(α+π/4)·cos(α+π/4)
tan2α = 2tanα/[1-(tanα)2]
三倍角
sin3α = 3sinα-4sin3α
cos3α = 4cos3α-3cosα
tan3α = (3tanα-tan3α)/(1-3tan2α)
sin3α = 4sinα·sin(π/3-α)·sin(π/3+α)
cos3α = 4cosα·cos(π/3-α)·cos(π/3+α)
tan3α = tanα·tan(π/3-α)·tan(π/3+α)
n倍角
根據棣莫弗定理的乘方形式(cos θ+i·sin θ)n=cos nθ+i·sin nθ (註:sin θ前的 i 是虛數單位,即-1開方)
將左邊用二項式定理展開分別整理實部和虛部可以得到下面兩組公式
sin(nα) = ncos(n-1)α·sinα - C(n,3)cos(n-3)α·sin3α + C(n,5)cos(n-5)α·sin5α-…
cos(nα) = cosnα - C(n,2)cos(n-2)α·sin2α + C(n,4)cos(n-4)α·sin4α
輔助角
Asinα+Bcosα = √(A2+B2)sin[α+arctan(B/A)]
Asinα+Bcosα = √(A2+B2)cos[α-arctan(A/B)]
半角公式
sin(α/2) = ±√[(1-cosα)/2]
cos(α/2) = ±√[(1+cosα)/2]
tan(α/2) = ±√[(1-cosα)/(1+cosα)]=sinα/(1+cosα)=(1-cosα)/sinα=cscα-cotα
cot(α/2) = ±√[(1+cosα)/(1-cosα)]=(1+cosα)/sinα=sinα/(1-cosα)=cscα+cotα
sec(α/2) = ±√[(2secα/(secα+1)]
csc(α/2) = ±√[(2secα/(secα-1)]
誘導公式
kπ+a
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(kπ+α)=tanα
cot(kπ+α)=cotα
sec(2kπ+α)=secα
csc(2kπ+α)=cscα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sec(π+α)=-secα
csc(π+α)=-cscα
-a
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sec(-α)=secα
csc(-α)=-cscα
π-a
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sec(π-α)=-secα
csc(π-α)=cscα
π/2±a
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sec(π/2+α)=-cscα
csc(π/2+α)=secα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sec(π/2-α)=cscα
csc(π/2-α)=secα
3π/2±a
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sec(3π/2+α)=cscα
csc(3π/2+α)=-secα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sec(3π/2-α)=-cscα
csc(3π/2-α)=-secα
恆等變形
tan(a+π/4)=(tan a+1)/(1-tan a)
tan(a-π/4)=(tan a-1)/(1+tan a)
asinx+bcosx=[√(a2+b2)]{[a/√(a2+b2)]sinx+[b/√(a2+b2)]cosx}=[√(a2+b2)]sin(x+y)【輔助角公式,其中tan y=b/a,或者說siny=b/[√(a2+b2)],cosy=a/[√(a2+b2)]】
萬能代換
積化和差
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ= -(1/2)[cos(α+β)-cos(α-β)](註:留意最前面是負號)
和差化積
內角公式
sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)
cosA+cosB+cosC=1+4sin(A/2)sin(B/2)sin(C/2)
tanA+tanB+tanC=tanAtanBtanC
cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)
tan(A/2)tan(B/2)+tan(B/2)tan(C/2)+tan(C/2)tan(A/2)=1
cotAcotB+cotBcotC+cotCcotA=1
(cosA)^2+(cosB)^2+(cosC)^2+2cosAcosBcosC=1
sin2A+sin2B+sin2C=4sinAsinBsinC
降冪公式
證明方法
首先,在三角形ABC中,角A,B,C所對邊分別為a,b,c若A,B均為銳角,則
在三角形ABC中,過C作AB邊垂線交AB於D 由CD=asinB=bsinA(
做另兩邊的垂線,同理)可證明正弦定理:a/sinA=b/sinB=c/sinC於是有:AD+BD=c AD=bcosA,BD=acosB AD+BD=c代入正弦定理,可得sinC=sin(180-C)=sin(A+B)=sinAcosB+sinBcosA 即在A,B均為銳角的情況下,可證明正
弦和的公式。利用正弦和
餘弦的定義及周期
性,可證明該公式對
任意角成立。於是有 cos(A+B)=sin(90-A-B)=sin(90-A)cos(-B)+cos(90-A)sin(-B)=cosAcosB-sinAsinB
由此求得以上全部公式