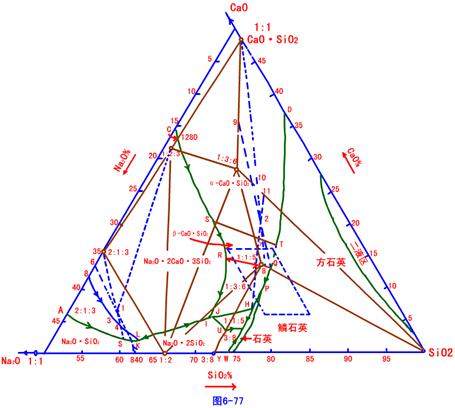
概述
含有三個組元的系統稱為三元系統,或稱三元系。如金屬材料中的Fe—C—Si、Fe—C—Cr、A1一Mg—Cu三元系合金,以及K
2O一Al
2O
3一SiO
2、CaO一Na
2O一SiO
2、三元系陶瓷。
三元系統與二元系統比較,組元數增加了一個。一般經驗告訴我們,由於組元間的相互作用,不能簡單地用二元系合金的性能來推斷三元系合金的性能,因為組元間的作用往往不是加和性的;在二元系中加入第三組元後會改變原來組元間的
溶解度。可能出現新的轉變。產生新的組相。這些材料的組織、性能和相應的加工、處理工藝等通常都不等同於二元系合金。因此,要研究三元系材料的成分、組織和性能間關係,需要首先了解三元系相圖。
對於二元系統,在恆壓條件下只有兩個獨立參量;溫度和成分,故二元相圖是一個平面圖形。對於三元系統.在恆壓下有三個獨立參量:溫度和兩個成分參數,所以三元相圖是一個立體圖形。構成三元相圖主要應該是一系列空間曲面及依此所圍成的空間區域,而不是二元相圖中那些平面曲線。所以,與二元相圖相比.三元相圖的類型多而複雜,至今比較完整的相圖只測出了十幾種,更多的是三元相圖中某些有用截面圖和投影圖。
三元相圖的表示方法
二元系統只有一個成分參數.因而只需一根直線坐標就可以表示二元系各種成分。三元系統有兩個成分參數,故只能用濃度平面來表示三元系的成分。通常採用的有等邊三角形、等腰三角形及直角三角形等表示。現分別討論如下:
等邊三角形法
取等邊三角形ABC,以其三個頂點表示三個純組元;三個邊各定為100%,分別代表三個二元素A—B、B—C和C—A的成分;位於三角形內部的點代表三元系的成分。此三角形稱為成分三角形或濃度三角形。
等腰三角形法
上述等邊三角形法套用較廣,其優點是成分標尺處處都是一致的。但若結合具體套用而從另外角度來看,優點卻可以變為缺點。例如當要研究的三元系合金不是全部,只是一部分,而且其中以兩個組元(例如A、B)為主,而第三組元(C)的濃度很低,這樣,這些合金的成分必然落在濃度三角形ABC靠AB邊的一條狹長帶上,套用諸多不便。這時,若將有關低濃度組元的兩個邊AC和BC的長度按同一比例擴大若干倍,例如10倍或5倍(也可以其它倍數),而變成一個等腰三角形,並取其中的一部分就方便多了。為適應改變後的新情況,標度和讀數順序也相應的有所變動。
直角三角形法
當要研究的三元系部分合金中,是以一個組元(例如A)為主,而其餘兩組元的濃度部相當低時,則多採用直角三角形法,即直坐標法。
三元系濃度三角形的性質
垂線、平行線定理 ·
從等邊三角形ABC內任一點P向三個邊畫三條垂線,這三條垂線之和等於三角形的高,即PG+PE+PF=AD。從等邊三角形ABC內任一點P畫三個邊的平行線,則三條平行線之和等於任一邊長,即:PM+PL+PK=AC(或AB或BC)。
 垂線、平行線定理 ·
垂線、平行線定理 ·等含量規則
在等邊三角形中畫一條平行於任一邊的線,則該條線任何一點有一個組元的成分是不變的,這個組元就是對應這個邊的頂點的物質。
 等含量規則
等含量規則定比例規則
從一頂點畫一條斜線到對邊,則該條斜線上的任何點,由其他二頂點所代表的二組分成分之比是不變的。
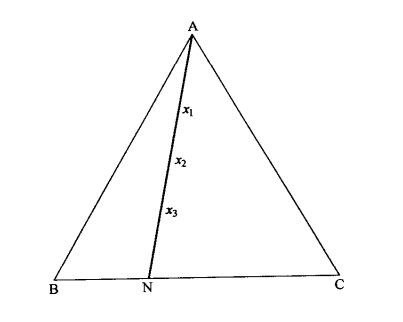 定比例規則
定比例規則直線規則
在三元系中,由兩個不同組成的體系D、E混合而成一個總體系F,則總體系F的組成點一定,在D、E兩體系的連線線上,而且兩體系的質量比由槓桿規則確定。
 直線規則
直線規則重心規則
在濃度三角形ABC內,若三個已知成分和質量的體系混合,他們在三元系相圖處於x,y,z位置,則其混合後所形成的新的體系P點位於這個三角形的重心位置。
 重心法則
重心法則 垂線、平行線定理 ·
垂線、平行線定理 · 等含量規則
等含量規則 定比例規則
定比例規則 直線規則
直線規則 重心法則
重心法則