巴申定律是巴申於1889年,從大量的實驗中總結出的擊穿電壓Ub與氣體壓力p、間隙d之間關係的定律。當時,人們並不知道氣體的電正性,它在後來被驗證,巴申定律也適用於電負性氣體。
基本介紹
- 中文名:巴申定律
- 外文名:Paschen's law
- 別稱:帕邢定律
- 表達式:Ub=f(pd)
- 提出者:弗里德里希·巴申
- 提出時間:1889年
- 套用學科:物理
- 適用領域範圍:高壓與絕緣
背景,原理,擊穿電壓,公式,
背景
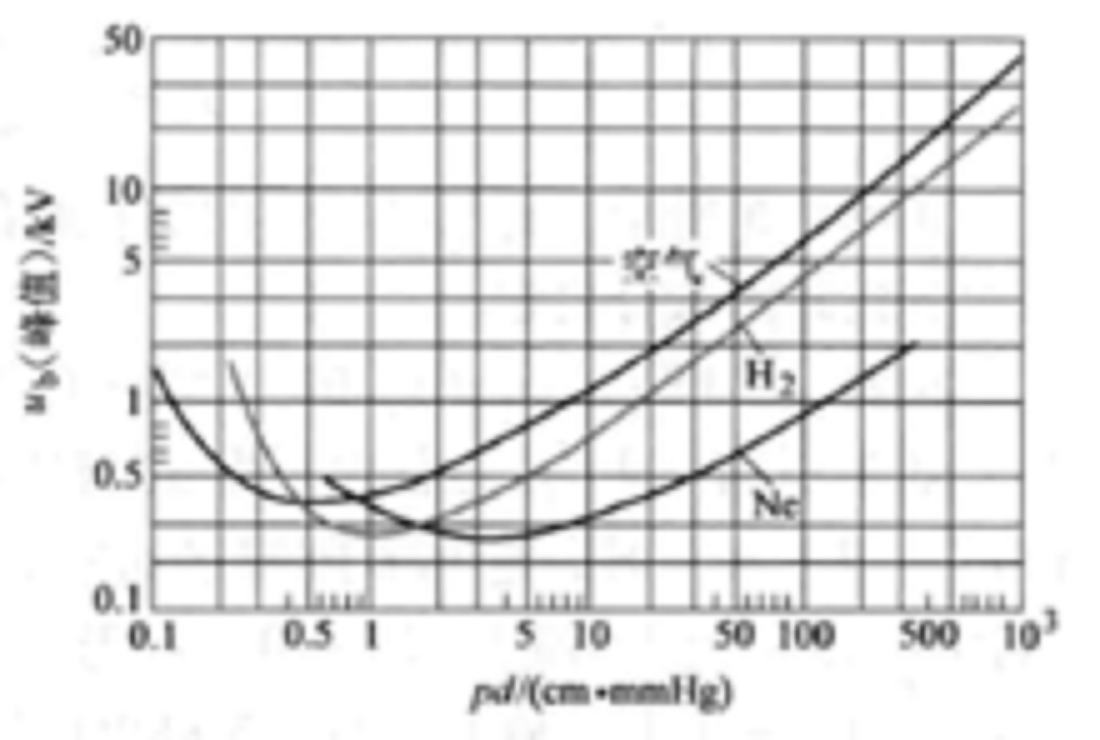
早在湯遜理論出現之前,巴申(Paschen)就於1889年從大量的實驗中總結出了擊穿電壓Ub與pd的關係曲線,其結果如下圖所示,稱為巴申定律,即
Ub=f(pd)
或
f2(Ub/pd){exp[pdf1(Ub/pd)-1]}=1
圖給出了空氣間隙的Ub與pd關係曲線,從圖中可見,首先,Ub並不僅僅由d決定,而是pd的函式;其次,Ub不是pd的單調函式,而是U形曲線,有極小值。
原理
大多數檢驗巴申定律的實驗是在控制低氣壓和小間隙的條件下進行的,其中電場的均勻程度,即Schwaiger因子η,可以很容易地在均勻電場中保持不變。從均勻到極不均勻的過渡過程中有一個稍不均勻場的電場分布情況,大氣壓下Schwaiger係數在0.25≤η<1的範圍內,均勻電場中的電介質特性與稍不均勻場很相似。
為了解釋此曲線的形狀,可以考慮固定間距(d=常數)的間隙,並且讓氣壓從曲線右邊下降到最小值。當氣壓降低時,氣體的密度降低,因此降低了向陽極進行中電子與分子碰撞機率。由於每次碰撞損失能量,弱電場強度或低壓損耗足以提供給電子足夠的動能,使其發生電離碰撞,並最終導致擊穿。
當達到最小擊穿電壓且氣壓繼續減小時,氣體的密度變得很低,碰撞發生很少。在這種情況下,即使電子的動能大於電離所需能量,電子碰撞也不一定能電離分子。通過電子碰撞引起的電離成功的機率大大減少。換言之,電子電離的有限機會取決於它的能量。只有通過增加電場強度使電離機率增大,擊穿才能發生。這解釋了為何擊穿電壓在左邊有最小值。在低壓下,出現高真空條件。因此,此區域的現象是適用於高壓真空管和開關的。在這些條件下,電極材料的擊穿電壓效應起著重要的作用。巴申定律不適應於曲線最左側部分。
擊穿電壓
氣隙的工作點不同時,擊穿電壓隨氣隙的變化規律也不同。可以這樣理解氣隙的擊穿:就是氣隙在外電壓作用下有強大電流通過,即有大量的帶電質點定向移動。而帶電質點的產生取決於從陰極出發的電子在向陽極移動過程中與中性質點的碰撞次數和使其游離的機率 。 假設氣壓保持不變 ,氣隙增大,則必須增大外設電壓才能使電子電子獲得足夠的能量易產生碰撞游離。但是當氣隙值很小,碰撞游離概論已經很高時,如果繼續減小,則由於電子與中性質點碰撞次數的減少,反而使氣隙移動的帶電質點減少,所以必須升高外設電壓才能保持氣隙的擊穿。 在氣隙變化過程中,總有一個氣隙距離值對氣隙中的帶電質點產生最有利,使擊穿電壓最小,這就是谷點,同理,當氣隙保持不變,氣體分子的相對密度增大時,電子的自由行程就縮短了,相鄰兩次碰撞之間積聚到足夠動能的機率減小了,故擊穿電壓必然升高,這就是谷點的右側。
巴申定律是反映間隙電壓耐受強度與氣體壓力和間隙之間的關係的定律。 其基本關係為:當氣體成分和電極材料一定時,氣體間隙擊穿電壓是氣壓和極間距離乘積的函式;當氣體溫度不定時,氣體間隙擊穿電壓是氣體密度和極間距離的函式。
公式
巴申定律是在氣體溫度不變的情況下得出的。對於氣體溫度並非恆定的情況,公式應改寫為
Ub=F(δd)
式中
δ——氣體相對密度,指氣體密度與標準大氣條件(Ps=101kPa,Ts=293K)下密度之比,即
δ=Tsp/Pst=2.9p/t
式中
p——擊穿實驗時氣壓,單位為kPa;
t——擊穿實驗時溫度,單位為K。