簡介
指獨立組分數為3的體系,該體系最多可能有四個
自由度,即溫度、
壓力和兩個濃度項,用
三維空間的立體模型已不足以表示這種
相圖。若維持壓力不變,則自由度最多等於3,其相圖可用立體模型表示。若壓力、溫度同時固定,則自由度最多為2,可用
平面圖來表示。通常在平面圖上用
等邊三角形(有時也有用
直角坐標表示的)來表示各組分的濃度。
工業上所使用的金屬材料,如各種合金鋼和有色合金,大多由兩種以上的組元構成,這些材料的組織,性能和相應的加工,處理工藝等通常不同於二元合金,因為在二元合金中加入第三組元後,會改變原合金組元間的溶解度,甚至會出現新的相變,產生新的組成相。
因此,為了更好地了解和掌握金屬材料,除了使用二元合金
相圖外,還需掌握三元甚至多元合金相圖,由於多元合金相圖的複雜性,在測定和分析等方面受到限制,因此,用的較多的是三元合金相圖,簡稱三元相圖(TernaryPhaseDiagram)。
三元相圖與二元相圖比較,組元數增加了1個,即成分變數是兩個,故表示成分的坐標軸應為2個,需要用一個平面表示,再加上垂直於該平面的溫度軸,這樣三元相圖就演變成一個在
三維空間的立體圖形,分隔相區的是一系列空間曲面,而不是二元相圖的平面曲線。
特定意義
等邊成分三角形中特定意義的線
平行於三角形某一邊的直線
凡成分位於該線上的所有合金,它們所含的由這條邊對應頂點所代表的組元的含量為一定值。
通過三角形頂點的任一直線
凡成分位於該直線上的所有合金,它們所含的由另兩個頂點所代表的兩組元的含量之比為一定值。
定量法則
套用相律f=c-p+1
當三元系時f=4-p
故當兩相平衡共存時,有f=4-2=2
即兩個平衡相的成分只有一個獨立改變,當一個平衡相的成分發生變化時,另一相的成分隨之而改變,即兩相的成分之間具有一定的關係,此關係稱為直線法則。
直線法則:三元合金中兩相平衡時,合金的成分點和兩個平衡相的成分點,必須在同一直線上。如圖5-105所示,當合金O在某一溫度處於α+β兩相平衡時,這兩個相的成分點便定為a和b,則aob三點必位於同一條直線上,且o點位於a,b兩點之間,此時α,β兩相的質量比為:
由直線法則可得到以下規律:
a:當溫度一定時,若已知兩平衡相的成分,則合金的成分必位於兩平衡相成分的連線上;
b:當溫度一定時,若已知一相的成分及合金的成分,則另一平衡相的成分必位於兩已知成分點的連線的延長線上;
c:當溫度變化時,兩平衡相的成分變化時,其連線一定繞合金的成分點而轉動;
表示方法
等邊成分三角形
常用三角形來表示三元合金的成分,這樣的三角形稱為濃度三角形或成分三角形(CompositionTriangle)。常用的成分三角形是
等邊三角形和直角三角形。
如圖所示:
 圖5-101
圖5-101oa+ob+oc=AB=BC=CA
由於oa=bC=WA
ob=Ac=WB
oc=Ba=WC
因此,可用
oa代表A組元的含量,
ob代表B組元的含量,
oc代表C組元的含量。
直角成分坐標表示法
當三元系成分以某一組元為主,其他兩個組元含量很少時,合金成分點將靠近
等邊三角形某一頂點。若採用
直角坐標表示成分,則可使該部分
相圖更為清楚的表示出來,一般用坐標原點代表高含量組元,而兩個互相垂直的坐標軸代表其他兩個組元的成分。
等腰成分三角形
當三元系中某一組元含量較少,而另兩組元含量較大時,合金成分點將靠近等邊成分三角形的某一邊。為了使該部分相圖清晰的表示出來,常採用等腰三角形,即將兩腰的刻度放大,而底邊的刻度不變。
對於O點成分的合金,其成分的確定方法與前述
等邊三角形的確定方法相同,即過O點分別引兩腰的
平行線與AC邊相交於a和c點,則:
Ca=WA=30%
Ac=WC=60%
Ab=WB=10%。
雖然,上述成分表示方法在三元
相圖中都有套用,但套用最為廣泛的還是等邊三角形。
三元系統相圖的基本類型
1、具有一個低共熔點的三元系統相圖
特點:三元組分各自在液態時完全互溶,而在固態時完全不互溶,不形成固溶體,也不形成化合物。只具有一個三元低共熔點。
2、生成一個一致熔融二元化合物的三元系統相圖
在相圖上的特點:其組成點位於其初晶區範圍內。
要求:
(1)確定溫度的變化方向;
(2)各界線的性質;
(3)會劃分各分三元系統;
(4)分析不同組成點的析晶路程,析 晶終點和析晶終產物;
(5)在E1E2界線上m點是溫度最高點。(連線規則)
m點:
CS連線上的溫度最低點,C-S系統的低共熔點;E1E2界線上的溫度最高點。稱:馬鞍點。
重要的規則——副三角形的劃分
副三角形——指與該無變數點液相平衡的三個晶相組成點連線成的三角形。
副三角形化的原則是要劃分出具有可操作的副三角形,即畫出的副三角形應有與其相對應的三元無變數點。
① 根據三元無變數點劃分,因為除多晶轉變和過渡點外,每個三元無變數點都有自己所對應的三角形,將與無變數點周圍三個初晶區相應的晶相組成點連線起來即可。
② 把相鄰兩個初晶區所對應的相組成連起來,不相鄰的不要連,這樣就可劃分出副三角形。
注意:與副三角形相對應的無變數點可以再該三角形內,亦可以在該三角形外,後者出現在不一致熔融化合物低的系統中。
3 具有不一致熔融二元化合物的三元系統
化合物組成點S不在其初晶區內。
S不穩定高溫分解。連線CS不代表真正二元系統,不能將系統分為二個分三元系統。
P點與E點不同,是個轉熔點:LP+B=C+S
分析:1點在S的初晶區內,開始析出晶相為S,組成點在△ASC內,析晶終點為E點,析出晶相為A、S、C;
2點在B的初晶區,開始析出的晶相為B,組成點在△BSC內,析晶終點為P點,析出晶相為B、S、C。
3點在C的初晶區內,開始析出的晶相為C,在△ASC內,析晶終點在E點,結晶終產物是A、S、C。途中經過P點,P點是轉熔點,同時也是過渡點。
4、生成一個固相分解的二元化合物的三元系統
1)形成高溫分解低溫穩定存在的二元化合物的三元相圖
特點:三個無變數點,但只能劃分兩個副三角形,即可能的析晶終點是P點或E點。
2)生成一個一致熔融三元化合物S
化合物組成點S在三元化合物初晶區內。
S:三元穩定化合物三個分三元系統
分析相圖的主要步驟
判讀相圖的步驟:
(1)判斷有多少化合物生成,判斷化合物的性質。
(2)用連線規則判斷界線溫度變化方向;
(3)用切線規則判斷界線性質;
(4)根據無變數點劃分相應的副三角形。
(5)確定無變數點的性質;
(6)分析析晶路程;
(7)判斷相圖上是否存在晶型轉變、液相分層或形成固溶體等現象。
複雜相圖處理辦法
(1)判斷化合物的性質——遇到一個複雜的三元相圖,首先要了解系統中有那些化合物,其組成點和初晶區的位置,然後根據組成點是否在它的初晶區內,判斷化合物的性質。
(2)劃分副三角形——根據劃分副三角形的原則和方法把三元相圖劃分為多個分三元系統,使複雜相圖簡化。
(3)判斷界線的溫度走向——根據連續規則判斷各條界線的溫降方向,並用箭頭標出。
(4)判斷界線性質——套用切線規則判斷界線是共熔性質還是轉熔性質,確定相平衡關係。共熔界線上用單箭頭,轉熔界線上用雙箭頭標出溫降方向以表示界線性質不同
(5)確定三元無變數點——根據三元無變數點與對應的副三角形的位置關係或根據交匯於三元無變數點的三條界線的溫度下降方向來判斷無變數性質,確定無變數點上的相平衡關係。
(6)分析冷卻析晶過程或加熱熔融過程——按照冷卻或加熱過程的相比規律,選擇一些系統點分析析晶或熔融過程。必要時用槓桿規則計算冷卻或加熱過程中平衡共存的各相含量。在分析冷卻析晶過程時要主要一下情況:① 系統組成點正好位於界線上時如何判斷初晶相?
首先判斷界線的性質,若界線是共熔線,則熔體冷卻時初晶相是界線兩側初晶區對應的兩個晶體,可用切線規則球的初晶相的瞬間組成;若界線是轉熔線,其熔體析晶時並不發生轉熔?(因為沒有任何晶體可轉熔),而使析出單一固相,液相組成點直接進入單相區(即某一晶體的初晶區)並按背向線規則變化。
② 系統組成點正好位於無變數點上時的初晶相是什麼?
若無變數點是三元低共熔點,則熔體析晶是共同析出該三組元的固相;若無變數點是單轉熔點,則其熔體析晶時在無變數點並不發生四相無變數過程,也不發生轉熔,而是液相組成點沿某一界線變化析晶,具體析晶性質由①點判斷;若無變數點是雙轉熔點,則其熔體析晶時在無變數點並不發生四相無變數過程,不發生轉熔,也不沿界線變化,而是析出單一固相,這時液相組成進入單相區並按照背向線規則變化。
 圖5-101
圖5-101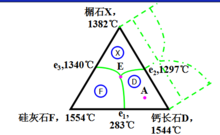


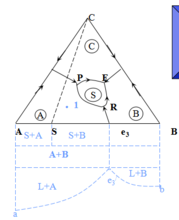


 圖5-101
圖5-101




