Matlab中的用法 solve(eq)
solve(eq, var)
solve(eq1, eq2, ..., eqn)
g = solve(eq1, eq2, ..., eqn, var1, var2, ..., varn)
其中,eq代表一個符號
表達式 或字元串,var代表一個變數名稱
詳細的解釋:
g=solve(eq)
函式求代數方程的符號解析解。參量eq表示符號表達式或字元串。若eq是一符號表達式或一沒有等號的字元串,則函式對方程的默認變數求解方程eq=0,默認變數由命令findsym(eq)確定。若輸出參量g為單一變數,則對於有多重解的非線性方程,g為一行向量。
g=solve(eq,var)
用法同上,var為指定變數。即對符號表達式或沒有等號的字元串eq中指定的變數var求解方程eq(var)=0。
g=solve(eq1,eq2,…,eqn)
函式求代數方程的符號解析解。參量eq1,eq2,…,eqn表示符號表達式或字元串。函式對方程組eq1,eq2,…,eqn中由命令findsym確定的n個變數如x1,x2,…,xn求解。若g為一單個變數,則g為一包含n個解的結構;若g為有n個變數的向量,則分別返回結果給相應的變數。
g=solve(eq1,eq2,…,eqn,var1,var2,…,varn)
用法同上,var1,var2,…,varn為指定變數,即對方程組eq1,eq2,…,eqn中指定的n個變數var1,var2,…,varn求解。
g= solve(eqn1,...,eqn,,var1,...,varn,Name,Value)
用法同上,Name和Value用來對解方程做一些更高級的控制 。不填時,按默認值求解。若要控制多個Name對應的Value值,沒有順序要求。Name和Value的選項如下。
Name
Value
'ReturnConditions'
默認為false,當為true時額外提供兩個參數。
Example: [v1, v2, params, conditions] = solve(sin(x) +y == 0,y^2 == 3,'ReturnConditions',true)
'IgnoreAnalyticConstraints'
默認為false,當為true時會先對原方程進行一些化簡操作後再解,以得到較為精簡的結果,這也有可能使一些原本用solve解不出來的方程可以得到解。但置為true時也有可能使解不完整或產生錯誤
'IgnoreProperties'
默認為false,當為true時求解時會忽略變數定義時的一些假設,比如假設變數為正(syms x positive)
'MaxDegree'
默認為3,當複雜多項式方程的階數高於'MaxDegree'時,solve可能 只給出隱式解 ,調整該項可以讓solve給出一些更高階代數方程的顯性解 。注意該項最大為4(在數學上更高階的多項式方程往往很少有解析解)
'PrincipalValue'
默認為false,為true時只給出一個主要的解
'Real'
默認為false,為true時只給出實數解
解單個方程 如果以x為變數
syms a b c x;solve('a*x^2 + b*x + c')%結果如下ans =-(b + (b^2 - 4*a*c)^(1/2))/(2*a) 如果以b為變數
syms a b c x;solve('a*x^2 + b*x + c','b')%結果如下ans =-(a*x^2 + c)/x 解方程組 syms x;S = solve('x + y = 1','x - 11*y = 5');S = [S.x S.y]%結果如下S =[ 4/3, -1/3] 解簡單的超越方程 對於一些簡單的超越方程,solve可以自動調用數值計算系統給出一個解,但可能不是完整的解 。
例子:
syms xsolve(sin(x) == x^2 - 1)
以上方程沒有解析解,故求解器自動調用數值計算系統試圖尋找數值解。但要想在整個定義域內尋根將要花費大量時間和資源,故solve只找出一個解。
結果:
ans =-0.63673265080528201088799090383828
如果對這個該函式畫圖後會發現其實這個方程是有兩個解的。
ezplot(sin(x), -2, 2)hold onezplot(x^2 - 1, -2, 2)hold off 為求出另一個根可以調用MuPAD的數值求解器,並
指明求解區間,或者用fsolve等其他方法數值求解,
下面用evalin函式調用MuPAD求解另一個在0~2之間的根
evalin(symengine, 'numeric::solve(sin(x) = x^2 - 1, x = 0..2)')
結果:
ans =1.4096240040025962492355939705895
高級控制的例子
syms xsolve(x^5 == 3125, x) 這樣就得到複數域上的5個解,結果:
ans =5(5*5^(1/2))/4 + (2^(1/2)*(5^(1/2) + 5)^(1/2)*5*i)/4 - 5/4(5*5^(1/2))/4 - (2^(1/2)*(5^(1/2) + 5)^(1/2)*5*i)/4 - 5/4(2^(1/2)*(5 - 5^(1/2))^(1/2)*5*i)/4 - (5*5^(1/2))/4 - 5/4- (2^(1/2)*(5 - 5^(1/2))^(1/2)*5*i)/4 - (5*5^(1/2))/4 - 5/4 如果只想要實數域上的解,那么在Name和Value的地方加上:
solve(x^5 == 3125, x, 'Real', true) 結果:
ans =
5
注意事項 1 solve解非代數方程的能力較弱,最好結合其他方式求解非代數方程
2 如果解得是一個方程組,而且採用了形如[a,b] =solve(a+b==1, 2*a-b==4,a,b) 的格式,那么,在MATLAB R2014a中沒問題,可以保證輸出的a,b就等於相應的解,但是在R2012b等早先版本中不能保證輸出的順序就是你聲明變數時的順序。所以最好採用g =solve(a+b==1, 2*a-b==4,a,b)這種單輸出格式,這樣輸出的是一個結構體,g.a 和g.b 就是對應的解。
MuPAD中的solve MuPAD是MATLAB現在的符號計算引擎(以前為maple),也可以單獨使用,單獨使用時語法有所不同。
語法 solve(eq, x, <Options>) 單個方程,指定變數
solve(eq, x = a .. b, <Options>) 單個方程,指定區間
solve(eq, vars, <Options>) 方程組
solve(eq, <Options>)
solve(system, x, <Options>)
solve(system, vars, <Options>)
solve(system, <Options>)
solve(ODE)
solve(REC)
解多項式方程 solve(x^7 + x^2 + x, x)
解多項式方程
解差分方程 R:=rec(eq, y(n), <cond>);solve(R)
eq:
方程或表達式
y:
未知函式
n:
索引號
cond:
初始值或邊界集合
由此可見,Rec主要是返回多項式的結果
表達式 ,對於複雜問題,有直接法,for多重循環,濾波器法,Z變換法。
解差分方程
解常微分方程 ode::solve(o, <Type = OdeType>, <Opts>)solve(o, <Type = OdeType>, <Opts>)
解常微分方程
Mathematica中Solve的用法 調用方法:Solve[expr,vars]
例:Solve[x^2 + a x + 1 == 0, x]

 解多項式方程
解多項式方程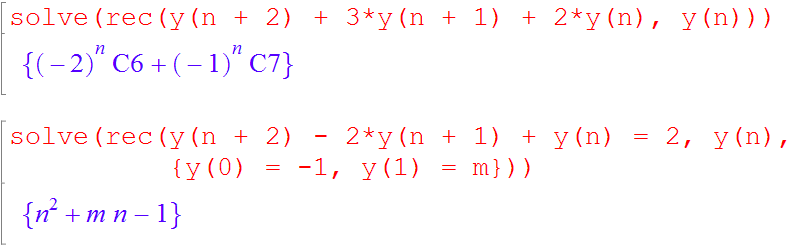 解差分方程
解差分方程 解常微分方程
解常微分方程
